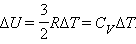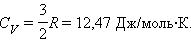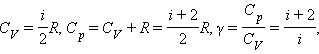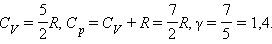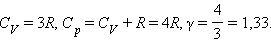что называется теплоемкостью газа
Что называется теплоемкостью газа
Во многих случаях удобно использовать молярную теплоемкость C :
Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.
Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: C V – молярная теплоемкость в изохорном процессе ( V = const) и C p – молярная теплоемкость в изобарном процессе ( p = const).
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
Изменение Δ U внутренней энергии газа прямо пропорционально изменению Δ T его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
Отношение Δ V / Δ T может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
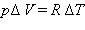
Молярная теплоемкость C p газа в процессе с постоянным давлением всегда больше молярной теплоемкости C V в процессе с постоянным объемом (рис. 3.10.1).
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой γ.
|
В частности, это отношение входит в формулу для адиабатического процесса (см. §3.9).
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией 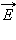
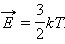 |
Внутренняя энергия 1 моля идеального газа равна произведению 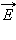
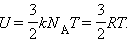 |
При изменении температуры на Δ T внутренняя энергия изменяется на величину
|
Коэффициент пропорциональности между Δ U и Δ T равен теплоемкости C V при постоянном давлении:
|
Это соотношение хорошо подтверждается в экспериментах с газами, состоящими из одноатомных молекул (гелий, неон, аргон). Однако, для двухатомных (водород, азот) и многоатомных (углекислый газ) газов это соотношение не согласуется с экспериментальными данными. Причина такого расхождения состоит в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию не только поступательного, но и вращательного движения молекул.
В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы :
Из этой теоремы следует, что молярные теплоемкости газа C p и C V и их отношение γ могут быть записаны в виде
|
где i – число степеней свободы газа.
Для газа, состоящего из одноатомных молекул ( i = 3)
|
Для газа, состоящего из двухатомных молекул ( i = 5)
|
Для газа, состоящего из многоатомных молекул ( i = 6)
|
Экспериментально измеренные теплоемкости многих газов при обычных условиях достаточно хорошо согласуются с приведенными выражениями. Однако, в целом классическая теория теплоемкости газов не может считаться вполне удовлетворительной. Существует много примеров значительных расхождений между теорией и экспериментом. Это объясняется тем, что классическая теория не в состоянии полностью учесть энергию, связанную с внутренними движениями в молекуле.
Поэтому молярная теплоемкость вещества в твердом состоянии равна:
|
Физика Б1.Б8.
Молекулярная физика и термодинамика
1. Введение
Основы молекулярной физики были заложены трудами Ломоносова, Джоуля, Больцмана, Клаузиуса, Максвелла и других ученых. Благодаря их трудам молекулярная физика прочно утвердилась в науке. Непосредственным опытным подтверждением молекулярно-кинетической теории являются процесс диффузии, броуновского движения, распространения запаха и многие другие явления.
Движение каждой молекулы в веществе может быть описано законами классической механики. Однако число молекул в веществе чрезвычайно велико, направления и величины скоростей молекул совершенно случайны и непрерывно изменяются так, что становится невозможным охватить уравнениями движения всю совокупность молекул и сделать какие-либо выводы об их поведении.
Тем не менее, состояние вещества и его изменение определяется заданием небольшого числа определенных параметров, как температура, давление, объем, плотность и т.д., значения которых невозможно указать на основе решений уравнений классической механики. Дело в том, что свойства огромного числа молекул подчиняется особым, статистическим закономерностям. Статистическая физика изучает статистические закономерности, описывающие поведение большой совокупности объектов. Она основывается на теории вероятностей и позволяет вычислять средние значения величин, характеризующих движение всей совокупности молекул (средние скорости молекул, средние кинетические энергии, средние значения импульса и т. д.) и на этой основе истолковывает свойства вещества, непосредственно наблюдаемые на опыте (давление, температура и т.д.). В этом состоит суть молекулярно-кинетического изучения вещества.
Наряду со статистическим, существует термодинамический метод изучения вещества. В отличие от статистического метода термодинамический метод не интересуется строением вещества. Термодинамика изучают условия превращения энергии и характеризует их с количественной стороны.
В основе термодинамики лежит небольшое число закономерностей, установленных на основе большого числа опытных фактов и получивших название начала термодинамики.
У статистической физики и термодинамики общий предмет изучения – свойства вещества и происходящие в нем процессы. Подходя к изучению этих свойств с разных точек зрения, эти методы взаимно дополняют друг друга.
Совокупность тел, могущих обмениваться энергией между собой и с внешними телами, не входящими в эту систему, называется термодинамической системой. Одним из основных понятий термодинамики является понятие состояния системы. Состояние системы определяется совокупностью значений всех величин, характеризующих физические свойства системы и называемых термодинамическими параметрами (температура, давление плотность, теплоемкость, электропроводность и т. д.). Состояние системы называется стационарным, если значения всех термодинамических параметров не изменяются во времени. Стационарное состояние называется равновесным, если его неизменность не обусловлена протеканием каких-либо процессов во внешних по отношению к данной системе телах.
Исследования показывают, что параметры состояния тел взаимно связаны и могут быть выражены друг через друга. Поэтому термодинамическое состояние задается только ограниченным числом параметров состояния. Такие параметры называются основными параметрами состояния. Важнейшими параметрами состояния химически однородных систем являются плотность, объем, давление, температура. И между этими параметрами существует связь, выражаемая в виде математического уравнения 
Теплоемкость газов



Теплоемкостью называется количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить температуру какой–либо количественной единицы его на 1 о С.
В зависимости от выбранной количественной единицы вещества различают:
мольную теплоемкость µс – кДж/(кмоль · К),
массовую теплоемкость с – кДж/(кг · К),
объемную теплоемкость с’ – кДж/(м 3 · К).
Как известно, 1 м 3 газа в зависимости от параметров его состояния имеет разные массы. В связи с этим объемную теплоемкость всегда относят к массе газа, заключенного в 1 м 3 его при нормальных условиях
[рн = 101325 Па (760 мм рт.ст.) и Тн = 273 К (tн = 0 °С)].
Для определения значений перечисленных выше теплоемкостей достаточно знать величину одной какой–либо из них. Удобнее всего иметь величину мольной теплоемкости.
Тогда массовая теплоемкость 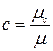
объемная теплоемкость 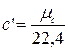
где 22,4 м 3 /кмоль – объем 1 кмоля всех идеальных газов при нормальных условиях.
Объемная и массовая теплоемкости связаны между собой зависимостью
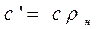
где 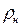
Теплоемкость газа зависит от температуры. По этому признаку различают среднюю и истинную теплоемкость.
Если q – количество теплоты, сообщаемой единице количества газа (или отнимаемого от него) при изменении температуры газа от t1 до t2 (или, что то же, от T1 до Т2), то
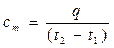
представляет собой среднюю теплоемкость в пределах t1…t2. Предел этого отношения, когда разность температур стремится к нулю, называют истинной теплоемкостью.
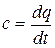
Теплоемкость идеальных газов зависит не только от их температуры, но и от их атомности и характера процесса. Теплоемкость реальных газов зависит от их природных свойств, характера процесса, температуры и давления.
Для газов особо важное значение имеют следующие два случая нагревания (охлаждения):
1) изменение состояния при постоянном объеме (по изохоре);
2) изменение состояния при постоянном давлении (по изобаре).
Обоим этим случаям соответствуют различные значения теплоемкостей.
В таблице 2.1 приведена классификация различных видов теплоемкостей в зависимости от единиц количества веществ (массовые, объемные и мольные), температуры (истинные и средние) и процесса (изохорные и изобарные).
Таблица 2.1 – Классификация теплоемкостей
| Теплоем– кость | Массовая кДж/(кг · К) | Объемная кДж/(м 3 · К) | Мольная кДж/(кмоль · К) | |||
| истин. | средняя | истин. | средняя | истин. | средняя | |
| Изохорная | сv | сvm | 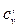 | 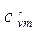 | µсv | µсvm |
| Изобарная | ср | сpm | 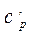 | 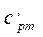 | µср | µсpm |
Еще в 1842 г. один из основоположников закона сохранения и превращения энергии Ю.Майер установил, что между мольными теплоемкостями при постоянном давлении и постоянном объеме существует следующая зависимость (закон Майера):
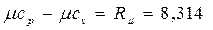
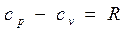
Физический смысл этой зависимости легко уяснить. Если для нагревания 1 моля (или 1 кг) газа в цилиндре над поршнем на 1 градус при постоянном объеме, т.е. при закрепленном поршне, надо затратить количество теплоты сv, то при постоянном давлении к этому количеству теплоты добавится работа Rµ (или R), которую будет совершать расширяющийся газ, толкая освобожденный поршень.
Для приближенных расчетов при невысоких температурах можно принимать следующие значения мольных теплоемкостей (таблица 2.2).
Отношение теплоемкостей при постоянных давлении и объеме обозначают к и называют коэффициентом Пуассона,илипоказателем адиабаты
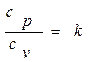
Таблица 2.2 – Приближенные значения мольных теплоемкостей при постоянном объеме и постоянном давлении (с = const)
| Газы | Теплоемкость, кДж/(моль·К) | |
| µсv | µср | |
| Одноатомные | 12,56 | 20,93 |
| Двухатомные | 20,93 | 29,31 |
| Трех– и многоатомные | 29,31 | 37,68 |
Согласно молекулярно–кинетической теории газов:
для одноатомных газов k = 1,667,
для двухатомных k = 1,4,
для трехатомных k = 1,29.
Теплоемкость газов изменяется с изменением температуры, при чем эта зависимость имеет криволинейный характер. В таблице 2.2 приведены теплоемкости для наиболее часто встречающихся в теплотехнических расчетах двух– и трехатомных газов.
При пользовании таблицами значения истинных теплоемкостей, а также средних теплоемкостей в пределах от 0° до t берут непосредственно из этих таблиц, причем в необходимых случаях производится интерполирование.
Количество теплоты, которое необходимо затратить в процессе нагревания 1 кг газа в интервале температур от t1 до t2,
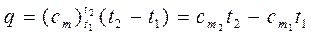
где 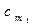
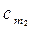
Из этой формулы легко получить выражение для определения количества теплоты, затрачиваемой в процессе при постоянном объеме и в процессе при постоянном давлении, т. е.
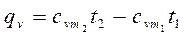
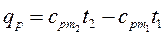
Если в процессе участвуют М кг или VН м 3 газа, то
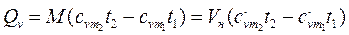
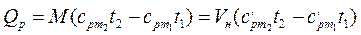
Теплоёмкость идеального газа
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.
Содержание
Молярная теплоемкость
Молярная теплоемкость — теплоемкость 1 моля идеального газа.
Теплоемкость идеального газа в изопроцессах
Адиабатический
В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть 

Следовательно, теплоемкость идеального газа в адиабатическом процессе равна нулю: 
Изотермический
В изотермическом процессе постоянна температура, то есть 
Изохорный
В изохорном процессе постоянен объем, то есть 

А для идеального газа
где 
Изобарный
В изобарном процессе (
Вывод формулы для теплоемкости в данном процессе
Согласно 1 началу термодинамики существует 2 способа изменить внутреннюю энергию тела (в нашем случае идеального газа): передать ему тепло или совершить над ним работу.
dU=δQ+δA, где δA — работа окр. среды над газом.
В расчете на 1 моль:
См. также
Полезное
Смотреть что такое «Теплоёмкость идеального газа» в других словарях:
Теплоёмкость — <<<Название>>> Размерность L2MT −2Θ−1 Единицы измерения … Википедия
ТЕПЛОЁМКОСТЬ — величина, равная отношению кол ва теплоты бQ, сообщаемого телу (системе) при бесконечно малом изменении его состояния в к. л. процессе, к соответствующему изменению темп ры Т этого тела: С = бQ/dT. Отношение Т. к массе тела т наз. удельной Т.: с … Большой энциклопедический политехнический словарь
Изобарная теплоёмкость — Теплоёмкость тела (обозначается C) физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT: Единица измерения теплоёмкости в системе СИ Дж/К.… … Википедия
Уравнение состояния газа Ван-дер-Ваальса — Уравнение состояния Статья является частью серии «Термодинамика». Уравнение состояния идеального газа Уравнение Ван дер Ваальса Уравнение Дитеричи Разделы термодинамики Начала термодинамики Уравнени … Википедия
Изобарная теплоемкость — Теплоёмкость тела (обозначается C) физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT: Единица измерения теплоёмкости в системе СИ Дж/К.… … Википедия
Закон равнораспределения — Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия
Эквипарциальная теорема — Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия
Теорема о равнораспределении — Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия
Цикл Стирлинга — Термодинамические циклы … Википедия
Статистическая физика — раздел физики, задача которого выразить свойства макроскопических тел, т. е. систем, состоящих из очень большого числа одинаковых частиц (молекул, атомов, электронов и т.д.), через свойства этих частиц и взаимодействие между ними.… … Большая советская энциклопедия