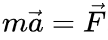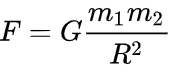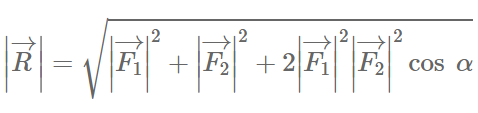что называется равнодействующей системы сил

Большая Энциклопедия Нефти и Газа

Равнодействующей системы сил называют силу, действие которой заменяет собой действие данной системы сил. Силу, образующую с равнодействующей уравновешенную систему сил, называют уравновешивающей силой. Замену одной силы несколькими называют разложением данной силы на составляющие. [2]

Равнодействующей системы сил называют силу, равную их векторной сумме и приложенную таким образом, что ее момент относительно любой точки пространства равен суммарному моменту этой системы сил. [3]

Равнодействующей системы сил называют силу, действие которой заменяет собой действие данной системы сил. Силу, образующую с равнодействующей уравновешенную систему сил, называют уравновешивающей силой. Замену одной силы несколькими называют разложением данной силы на составляющие. [5]

Если равнодействующая система сил существует, то вектор-момент равнодействующей данной системы сил относительно любой точки равен сумме векторов-моментов всех сил этой системы относительно той же точки. [6]

Работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том же участке пути. [7]

Работа равнодействующей системы сил на некотором пути равна сумме работ составляющих сил на том же пути. [8]

Теорема 12.1. Работа равнодействующей системы сил на некотором пути равна сумме работ составляющих сил на том же пути. [10]

Определим величину и положение точки приложения равнодействующей системы сил инерции элементов стержня при его вращении относительно оси с некоторой угловой скоростью. [13]

Источник

равнодействующая системы сил

Смотреть что такое «равнодействующая системы сил» в других словарях:

равнодействующая системы сил — равнодействующая Сила, эквивалентная данной системе сил. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика Обобщающие термины … Справочник технического переводчика

равнодействующая системы сил — равнодействующая системы сил; равнодействующая Сила, эквивалентная данной системе сил … Политехнический терминологический толковый словарь

РАВНОДЕЙСТВУЮЩАЯ — системы сил, сила, эквивалентная данной системе сил и равная их геом. сумме: R=SFk. Система сил, приложенных в одной точке, всегда имеет Р., если R?0. Любая другая система сил, приложенных к телу, если R?0, имеет Р., когда главный момент этой… … Физическая энциклопедия

РАВНОДЕЙСТВУЮЩАЯ — системы сил сила, оказывающая на твердое тело такое же механическое действие, как и данная система приложенных к телу сил. В простейших случаях (напр., для сил, приложенных в одной точке или расположенных в одной плоскости) равнодействующую можно … Большой Энциклопедический словарь

равнодействующая — системы сил; равнодействующая Сила, эквивалентная данной системе сил … Политехнический терминологический толковый словарь

РАВНОДЕЙСТВУЮЩАЯ СИЛА — сила, механическое действие которой на твёрдое тело эквивалентно действию данной системы сил, приложенных к этому телу. Отдельные силы системы называют составляющими (они характеризуются значением и направлением действия). Векторная сумма всех… … Большая политехническая энциклопедия

РАВНОДЕЙСТВУЮЩАЯ — системы сил сила, к рая по её влиянию на движение твёрдого тела полностью эквивалентна рассматриваемой системе сил, прилож. к телу. Система сил имеет Р, только в том случае, если для неё существует такой центр приведения (см. Приведение сил),… … Большой энциклопедический политехнический словарь

Равнодействующая — системы сил, сила, эквивалентная данной системе сил и равная их геометрической сумме: R = ∑Fk. Система сил, приложенных к одной точке, всегда имеет P., если R ≠ 0. Любая другая система сил, приложенных к телу, если R ≠ 0, имеет P., когда… … Большая советская энциклопедия

РАВНОДЕЙСТВУЮЩАЯ — системы сил, сила, оказывающая на тв. тело такое же механич. действие, как и данная система приложенных к телу сил. В простейших случаях (напр., для сил, приложенных в одной точке или расположенных в одной плоскости) Р. можно найти,… … Естествознание. Энциклопедический словарь

РАВНОДЕЙСТВУЮЩАЯ — ей; ж. Физ. = Равнодействующая сила. * * * РАВНОДЕЙСТВУЮЩАЯ РАВНОДЕЙСТВУЮЩАЯ системы сил, сила, оказывающая на твердое тело такое же механическое действие, как и данная система приложенных к телу сил. В простейших случаях (напр., для сил,… … Энциклопедический словарь

Источник

Что называется равнодействующей системы сил

Теоретическая механика – это наука о механическом движении твердых материальных тел и их взаимодействии. Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.

Статика изучает условия равновесия тел под действием сил.

Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.

Динамика изучает движение тел под действием сил.

Сила – это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т. е. сила – это величина векторная, характеризующаяся точкой приложения, направлением (линией действия), величиной (модулем).

Силы, действующие на тело (или систему сил), делят на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.

Системой сил называют совокупность сил, действующих на тело.

Эквивалентная система сил – система сил, действующая так же, как заданная.

Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.

Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.

Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами.

Первая аксиома. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).

Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются.

Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешивающую систему сил (принцип отбрасывания системы сил, эквивалентной нулю).

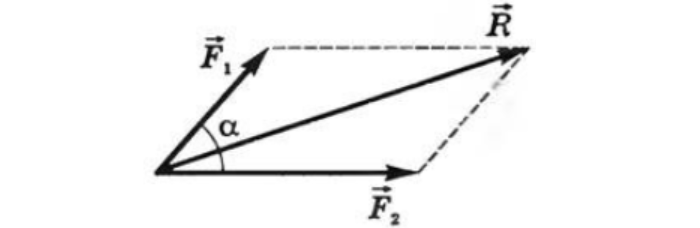
Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.

Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.

Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия.

2. Связи и реакции связей

Все тела делятся на свободные и связанные.

Свободные тела – это тела, перемещение которых не ограничено.

Связанные тела – это тела, перемещение которых ограничено другими телами.

Тела, ограничивающие перемещение других тел, называют связями.

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.

Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).

Связи делятся на несколько типов.

Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.

Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.

Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.

Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.

Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.

Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.

Неподвижный шарнир. Точка крепления перемещаться не может.

Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (R_x, R_y).

Защемление, или «заделка». Любые перемещения точки крепления невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реактивный момент М_z, препятствующий повороту.

Реактивная сила представляется в виде двух составляющих вдоль осей координат:

3. Определение равнодействующей геометрическим способом

Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Необходимо определить равнодействующую системы сходящихся сил (F₁; F₂; F₃;…; F_n), где n – число сил, входящих в систему.

В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.

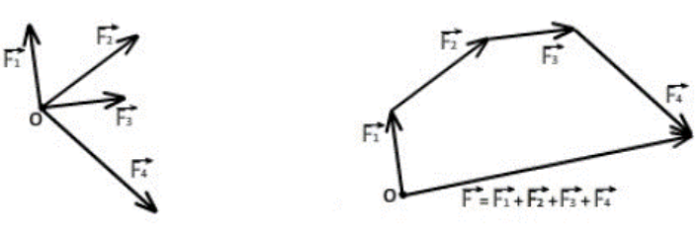
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.

Многоугольник сил строится в следующем порядке.

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).

Задачи решаются в следующем порядке.

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.

4. Определение равнодействующей аналитическим способом

Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.

Проекция силы на две взаимно перпендикулярные оси.

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.

Модуль (величину) равнодействующей можно определить по известным проекциям:

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской системы сходящихся сил:

При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

5. Пара сил. Момент силы

Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.

Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом. Силы, входящие в пару, не уравновешиваются, так как они приложены к двум точкам.

Действие этих сил на тело не может быть заменено одной равнодействующей силой.

Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил плеча пары.

Источник

Теоретическая механика

4. Система сходящихся сил

Условие равновесия сходящейся системы сил

Пусть на тело действует сходящаяся система сил (рис. С14).

На основании следствия из аксиомы №2 перенесем все силы в точку пересечения линий действия сил О.

Уравнение (С.1) является уравнением равновесия сходящейся системы сил в векторной форме.

Запишем условие равновесия в координатной форме. Для этого разложим все действующие силы по осям координат

Тогда в соответствие с уравнением (С.1) можно записать

Из формулы (С.4) следует, что вектор равен нулю, значит и проекции вектора на оси координат тоже равны нулю

Система уравнений (С.5) является координатной формой записи условия равновесия сходящейся системы сил.

Груз в виде шара подвешен на нити, как указано на рис.С.16.

Источник

Для рассмотрения термина «равнодействующая сила» придется воспользоваться некими абстрактными понятиями физики, теоретической механики. Упрощениями, условно отражающими реальный мир

Итак, примем во внимание, что:

Под объектом понимается не физическое тело с объемом, формой и внутренней структурой. Подразумевается «материальная точка», характеризующаяся только массой. То есть величиной, определяющей инерцию (стремление сохранять неподвижность) и гравитационные взаимодействия (притяжение предметов). Не стоит путать с весом. Последний является проявлением гравитации и меняется в зависимости от места измерения (географической широты).

События и наблюдения происходят в инерциальной системе отсчета. Где пространство и время однородны (идентичны в любой точке). Поворот системы отсчета не влияет на измерения.

Рассуждения корректны для скоростей существенно ниже скорости света и не распространяются на субатомный уровень.

Понятие силы

Возникло еще в трудах древнегреческих ученых. Носило скорее философский характер и было довольно запутанным и неоднозначным, что не мешало при этом античным инженерам-практикам производить весьма точные расчеты, поскольку понимание силы как причины движения было для них безусловным.

Позже проблемой занимались такие титаны как Роджер Бэкон и Уильям Оккам (английские философы и естествоиспытатели). Опять-таки без строгого физического подхода, но с более глубоким пониманием темы (теория «дальнодействия»).

Бэкман, Декарт, Галилей аргументированно оспорили архаичные теории. Классическая механика пробивала дорогу.

Иоганн Кеплер также придавал сначала силе эзотерические свойства. Но наблюдения за закономерностями перемещения небесных тел убили плохого теолога и породили ученого. Логично появилась идея общей силы тяготения. До Ньютона, вопреки распространенному заблуждению.

Ньютон подытожил и объединил ранее накопленные знания. Установил формулу зависимости действующей на тело силы с его движением (II-ой закон).

F – вектор (также имеется направление приложения) силы. В принятой РФ системе СИ (ISQ) измеряется в Ньютонах (Н, N в международном написании);

m – масса материальной точки (кг);

a – вектор получаемого ускорения (м/с 2 ).

При этом определение силы дано не было. Оно и понятно: явление не существует само по себе. Термин появился только для удобства расчетов и подразумевает меру воздействия стороннего тела или поля на наблюдаемый объект.

Возможно, что гравитация является действием поля. Закон всемирного тяготения был введен также Ньютоном.

· G – гравитационная постоянная;

· m₁, m₂ – массы материальных точек (кг);

· R – дистанция между объектами (м).

Тяготение Земли рассчитывается по традиционной формуле II-го закона Ньютона. Только «a» меняется на ускорение свободного падения «g».

Как измерить силу

В соответствии с I-м законом Ньютона, в инерциальных системах отсчета тело движется равномерно и прямолинейно либо покоится при отсутствии приложенных к нему сил. Или эти силы чем-то скомпенсированы.

Уравновесить усилие можно калиброванной пружиной, динамометром. Это статический способ. Типичный пример – замер силы тяжести при помощи весов.

Рассчитать силу можно, зная массу предмета и его ускорение. II-ой закон в помощь. В этом состоит динамический метод.

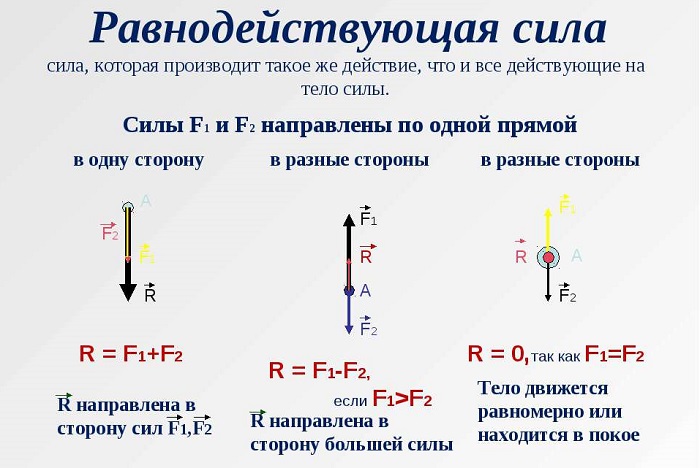
Равнодействующая сила

Если действуют несколько факторов одновременно, то результирующую силу можно найти по геометрическим правилам сложения.

Результат будет называться «вектор равнодействующей всех сил».

Примеры решения задач

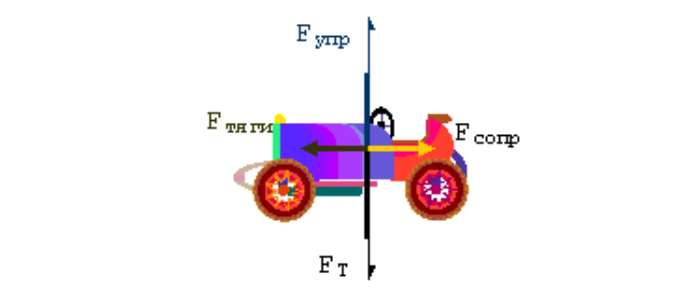
Сила тяжести направлена вертикально вниз. Модуль определяется следующим образом:

F_т = mg = 1000 (кг) х 9,81 (м/с 2 ) = 9810 (Н).

Упругая реакция дороги направлена противоположно и равна тяготению, поскольку движение в данной плоскости отсутствует и равнодействующая равна нулю.

F = ma = 1000 (кг) х 1 (м/с 2 ) = 1000 (Н).

F_cопр = F_тяги – F = 1500 (Н) – 1000 (Н) = 500 (Н).

Заключение

Несколько выводов напоследок:

Состояние покоя и прямолинейное равномерное движение механически аналогичны.

Сила придает телу ускорение, зависящее от массы объекта.

Равнодействующая образуется геометрическим суммированием приложенных к материальной точке векторов сил.

Источник