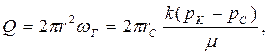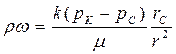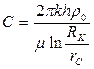что называется одномерным фильтрационным потоком

Добыча нефти и газа

Изучаем тонкости нефтегазового дела ВМЕСТЕ!

Установившаяся ПОТЕНЦИАЛЬНАЯ одномерная фильтрация

Установившаяся ПОТЕНЦИАЛЬНАЯ одномерная фильтрация

При данных условиях

3.1. Виды одномерных потоков

Одномерным называется поток, в котором параметры являются функцией только одной пространственной координаты, направленной по линии тока. К одномерным потокам относятся:

3.1.1. Описание одномерных потоков

Рис. 3.1. Схема прямолинейно-параллельного течения

б) Поток между круговыми батареями нагнетательных и эксплуатационных скважин в случае больших радиусов батарей (угол схождения векторов скорости бесконечно мал). При этом толщина пласта постоянна, а его кровля и подошва непроницаемы.

в) в лабораторных условиях при течении через цилиндрический керн или прямую трубу постоянного сечения, заполненную пористой средой или трещинной средой.

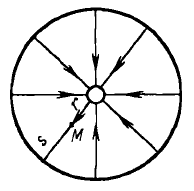
Рис. 3.2. Схема плоско-радиального

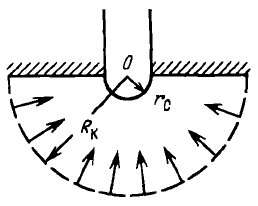
Рис. 3.3. Схема радиально-сферического течения

Такой поток может реализовываться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта (рис.3.3). Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта.

Описанные три вида одномерного потока играют большую роль при решении многих задач нефтегазопромысловой практики. Они лежат в основе ряда исследований закономерностей течения жидкости в пласте, в зависимости от принятой системы разработки или от конструктивных особенностей скважин. Естественно, моделируя каждый из трёх видов одномерного потока, мы прибегаем к некоторой схематизации реальных пластов и течений жидкости. Тем не менее, рассмотренные схемы не только воспроизводят, хотя и приближенно простейшие случаи течения жидкости в реальном пласте, но и помогают изучать более сложные виды потоков пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно представить себе состоящим из простейших видов потока.

Источник

Одномерные фильтрационные потоки несжимаемой жидкости в однородном пласте

Одномерным называется фильтрационный поток жидкости, в котором скорость фильтрации и напор являются функциями только одной координаты, отсчитываемой вдоль линии тока.

К одномерным относятся следующие потоки.

1. Прямолинейно-параллельный фильтрационный поток.

Контур питания для одной скважины – это условный контур, окружающий скважину, за пределами которого можно пренебречь возмущающим влиянием добывающей скважины. Для одиночной скважины – таким контуром является окружность такого радиуса, при котором на ней Р = Р_пл = P_k и w = 0. Для прямолинейной батареи скважины контур питания (условия на котором Р = Р_k и w = 0 сохраняются) также становится прямолинейным.

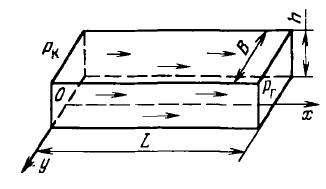
Для прямолинейно-параллельного фильтрационного потока линии тока жидкости в плане пласта и в его продольном сечении являются прямыми линиями, а скорость v в любой точке вертикального сечения пласта одинакова. Такой фильтрационный поток возникает при эксплуатации однородного пласта прямоугольной формы, у которого на контуре питания поддерживается постоянным давление Р_к, а батарея скважин, у которых давление на забое Р_r, расположена параллельно контуру питания (рис.10.1).

Рис. 10.1 План модели (а) и разрез по линии OX (б)

2. ) Плоскорадиальный параллельный фильтрационный поток.

Особенность плоскорадиального потока заключается в том, что линии тока совпадают с радиусами, сходящимися к центру окружности (скважине) и находятся в одной плоскости. В любом горизонтальном сечении пласта поведение линий тока одинаково. Плоскорадиальный поток создается в однородном круговом пласте постоянной мощности или пласте

1) Радиально-сферический фильт

3. Радиально-сферический фильтрационный поток.

Линии тока этого потока сходятся к центру сферы. Такой поток будет в пласте неограниченной мощности, вскрытом скважиной, имеющей полусферический забой (рис. 10.4).

Описанные три вида фильтрационных потоков являются простейшими моделями реальных течений, возникающих при разработке месторождений и играющих важную роль для практических расчетов.

Задача исследования заключается в определении гидродинамических характеристик: дебита (или расхода), давления, grad P и скорости фильтрации в каждой точке пласта, а также в установлении закона движения частиц вдоль их траекторий, и определения средневзвешенного по объему порового пространства пластового давления.

3.5.1. Прямолинейно-параллельный фильтрационный поток.

Пусть в горизонтальном пласте толщины h и ширины В в сечении I-I, совпадающем с контуром питания, поддерживается постоянное давление Р_к, а в сечении II-II, отстоящем на L_к, поддерживается давление Р_r в батарее добывающих скважин (рис. 10.1).

Дифференциальное уравнение Лапласа для такого течения: , т.к. фильтрация осуществляется вдоль оси х и производные по другим направлениям равны 0.

Интегрируя дважды, имеем:

.

Постоянные интегрирования определим из граничных условий (начальных условий нет, т.к. движение установившееся, т.е. не зависит от t).

.

Решением уравнения Лапласа будет функция Р(х) (распределение давления):

.

Находим из уравнения движения скорость фильтрации в пласте

.

Находим объемный расход жидкости в потоке как произведение скорости фильтрации w на площадь поперечного сечения пласта S = Bh, т.е.

.

Находим закон движения t = f (x), используя связь между скоростью фильтрации и скоростью движения частиц жидкости

.

Интегрируя по t от 0 до t и по х от 0 до х, получим

.

Вычисляем средневзвешенное по объему порового пространства пластовое давление

.

Поведение найденных характеристик плоскопараллельного фильтрационного процесса показано на рис. 10.5 и рис.10.6.

При фильтрации давление равномерно падает от P_k до P_r. Линии равного давления (изобары) на плоскости перпендикулярны кровле и почве пласта и равноотстоят друг от друга. Линии тока жидкости являются параллельными прямыми и перпендикулярны к изобарам. Поведение изобар и линий тока жидкости в пласте определяет гидродинамическое поле данного фильтрационного потока (рис. 10.6).

Лекция № 11

3.5.2 Плоскорадиальный фильтрационный поток.

Лекция № 11

Будем считать, что несжимаемая жидкость притекает к гидродинамической совершенной скважине радиусом r_c, расположенной в центре однородного горизонтального кругового пласта, толщиной h. На внешней круговой границе пласта радиусом R_k, служащей контуром питания, поддерживается постоянное давление P_k, на забое скважины давление Р_с тоже постоянно. Дифференциальное уравнение Лапласа в случае плоскорадиального фильтрационного потока имеет вид

.

Удобно перейти и решить задачу в цилиндрической системе координат (r,j,z) (рис. 11.1).

Уравнение Лапласа в криволинейной системе ( цилиндрической) системе координат:

Линии тока жидкости для данной фильтрационной модели совпадают с радиусами окружности (рис. 11.2). Поэтому в уравнении Лапласа останется одно слагаемое, зависимое от координаты r, и после подстановки в него значений коэффициентов Ляме примет вид:

Получаем

.

Это и есть дифференциальное уравнение Лапласа в цилиндрических полярных координатах для установившегося плоскорадиального течения несжимаемой жидкости по закону Дарси.

Дважды проинтегрировав дифференциальное уравнение, получаем

.

Постоянные интегрирования С₁, С₂ находим как обычно из граничных условий Р = Р_c при r = r_c; Р = Р_к при r = R_k.

Подставляя граничные условия, получаем систему уравнений для нахождения С₁, С₂:

.

Подставляя найденные значения С₁ и С₂ в решение, получим зависимость давления от координаты r в плоскорадиальном потоке.

.

Находим градиент давления

и используем его для нахождения скорости фильтрации

,

где: S = 2prh – поверхность фильтрации (боковая поверхность цилиндра радиуса r и высотой h) (рис. 11.3).

Формула — называется формулой Дюпюи.

Находим закон движения частиц из связи ; . Подставляя сюда значение w и интегрируя от 0 до t и от R0 до переменного r получим:

где: R₀ – начальное положение частицы в момент t = 0 и r – текущее положение в момент t.

.

Находим средневзвешенное по объему порового пространства пластовое давление

Прокомментируем некоторые результаты.

Дебит скважины пропорционален депрессии DР (разнице давлений в пласте и на забое работающей скважины) и одинаков через любую цилиндрическую поверхность, соосную со скважиной т.е. не зависит от r.

Отношение объемного дебита скважины к DР называется коэффициентом продуктивности

;

_.Через этот коэффициент дебит скважины выражается уравнением

Градиент давления и скорости фильтрации ведут себя одинаково и резко возрастают при приближении к скважине (рис. 11.5).

Логарифмическая кривая давления, вращение которой вокруг скважины образует поверхность, называется воронкой депрессии. Основная часть депрессии образуется в призабойной зоне, параметры которой сильно влияют на дебит скважины (рис. 11.6).

Гидродинамическое поле плоскорадиального потока описывается семействами изобар и линий тока. Изобара представляет окружности, поскольку, Р

= const- уравнение окружности. Линии тока – прямые, совпадающие с радиусами. Все выведенные формулы с заменой (Р_к – Р_с) на (Р_с – Р_к) справедливы для нагнетательных скважин.

3.5.3 Радиально-сферический фильтрационный поток

Лекция № 12

Будем считать, что несжимаемая жидкость притекает к скважине, вскрывающей бесконечный по мощности однородный пласт, через сферический забой радиуса r_c. Схема такого потока изображена на рисунке 12.1.

H_r = 1; H_q = r; H_j = r sinq.

Для рассматриваемой модели линии тока жидкости совпадают с радиусами полусферы, поэтому В уравнении Лапласа частные производные по координатам q и j равны 0 и уравнение Лапласа будет иметь вид:

и и .

Далее схема решения и нахождения характеристик потока жидкости полностью аналогична плоскорадиальному потоку. Дважды интегрируя, получим

Постоянные С₁ и С₂ определяем из граничных условий:

Подставив граничные условия, находим С₁ и С₂ из системы уравнений:

После подстановки значений С₁ и С₂ в общее решение, получим распределение давления в потоке несжимаемой жидкости как функции от координаты r

.

Если сопоставить формулы распределения давления для плоскорадиального и радиально-сферического потоков, то нетрудно заметить, что они имеют одинаковую структуру и переходят друг в друга, если логарифм отношения расстояний заменить разностью обратных значений расстояний:

.

Такое подобие структур формул характерно для выражений всех гидродинамических характеристик. Поэтому все остальные характеристики радиально-сферического потока (объемный расход несжимаемой жидкости, распределение скорости фильтрации, средневзвешенное давление и др.) можно получить из характеристик плоскорадиальной фильтрации аналогичной заменой в соответствующих формулах.

Источник

Описание одномерных потоков. Схемы одномерных фильтрационных потоков

— прямолинейно-параллельный фильтрационный поток;

— плоскорадиальный фильтрационный поток;

— радиально-сферический фильтрационный поток.

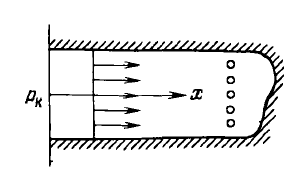
Приведем краткое описание этих потоков. Прямолинейно-параллельный фильтрационный поток. Предположим, что при фильтрации флюида траектории всех частиц параллельны, а скорости фильтрации во всех точках любого поперечного (перпендикулярного линиям тока) сечения равны друг другу. Законы движения вдоль всех траекторий такого фильтрационного потокоодинаковы, а поэтому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат ось х (рисунок 1.1). Прямолинейно-параллельный поток имеет место в лабораторных условиях при движении жидкости или газа через цилиндрический керн или через прямую трубу постоянного диаметра, заполненную пористой средой; на отдельных участках продуктивного пласта при движении жидкости к батарее скважин, если пласт постоянной толщины имеет в плане форму прямоугольника (смотри рисунок 1.1). Линии тока будут искривляться только вблизи скважин. Если уплотнить сетку скважин в батарее заменить батарею сплошной прямолинейной выработкой галереей, то движение к галерее будет строго прямолинейно-параллельным. Поток можно считать прямолинейно-параллельным на некотором участке между нагнетательной и добывающей батареями скважин.

Рисунок 1.1: Схема прямолинейно-параллельного потока к батарее скважин.

Рисунок 1.2: Схема прямолинейно-параллельного течения в пласте.

Плоскорадиальный фильтрационный поток. Предположим, что имеется горизонтальный пласт постоянной толщины h и неограниченной или ограниченной протяженности. В пласте пробурена одна скважина, вскрывшая его на всю толщину и имеющая открытый забой. При отборе жидкости или газа их частицы будут двигаться по горизонтальным траекториям, радиально сходящимся к скважине. Такой фильтрационный поток называется плоскорадиальным. Картина линий тока в любой горизонтальной плоскости будет одинакова, и для полной характеристики потока достаточно изучить движение флюида в одной горизонтальной плоскости. В плоскорадиальном одномерном потоке давление и скорость фильтрации в любой точке зависят только от

расстояния r данной точки от оси скважины.

а) 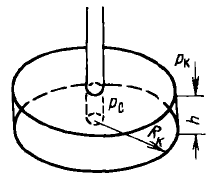б)

Рисунок 1.3: Схема плоскорадиального потока в круговом пласте: a) Общий вид; б) план.

Дата добавления: 2016-08-06 ; просмотров: 6573 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Характеристики одномерных фильтрационных потоков жидкости и газов

Для расчета перечисленных характеристик одномерных фильтрационных потоков жидкости и газа можно использовать два подхода. Первый из них – вывод дифференциальных уравнений и их решение отдельно для прямолинейно-параллельного, плоскорадиального и радиально-сферического потоков жидкости и газа. Второй – вывод обобщенного уравнения одномерного течения флюида в недеформируемой трубке тока переменного сечения с использованием функции Лейбензона и получение из него конкретных формул применительно к различным схемам фильтрационных потоков. Второй подход более эффективен, позволяет исходить из обобщенных характеристик течения, он был использован и при выводе следующих характеристик:

Прямолинейно – параллельная фильтрация несжимаемой жидкости

Схема прямолинейно-параллельного одномерного течения несжимаемой однородной ньютоновской жидкости в изотропном недеформируемом пласте (рис.). Пусть пласт представляет собой прямоугольный параллелепипед, шириной В и толщиной h, ограниченный сверху снизу непроницаемыми плоскостями, слева контуром питания, справа – галереей.

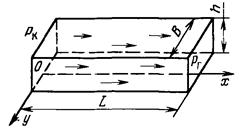
Площадь поперечного сечения 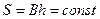; на контуре питания x₁ = 0, р₁ = р_K, на галерее x₂ = L, р₂ = р_Г.

Название контур питания обусловлено тем, что через плоскость х = 0 происходит приток в пласт жидкости, которая далее фильтруется к галерее x = L. Ось х направляем параллельно вектору скорости фильтрации.

, (3.1)

, (3.2, 3.3)

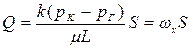
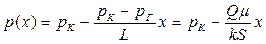
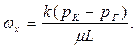
Давление в пласте при прямолинейно-параллельной фильтрации распределено по линейному закону, а скорость фильтрации во всем пласте постоянна.

При определении фильтрационных характеристик пласта по методу установившихся отборов строится индикаторная линия, которая представляет график зависимости расхода от разности давлений на контуре питания и галерее. Эта разность называется депрессией на пласт. Таким образом, индикаторная линия представляет собой график зависимости вида ,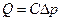

где С – коэффициент продуктивности. .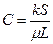

Следовательно, при выполнении закона Дарси индикаторная линия представляется в виде прямой линии.

Еще одна промысловая задача связана с определением времени движения в пласте «меченых частиц». Для этого в фильтрационный поток добавляют изотопы некоторых атомов или другие частицы, которые можно идентифицировать с помощью специальных методов. Время движения «меченых частиц» определяется из закона движения с помощью определения истинной средней скорости.

Если пористоть равна просветности, то время, за которое «меченая частица» переместиться от контура питания до произвольной точке в пласте

(3.4)

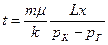
Время, за которое «меченая частица» переместиться от контура питания до галереи или время прохождения всего пласта

(3.5)

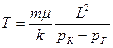
где m – пористость, k – проницаемость пористостых сред.

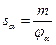
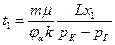
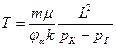
Если пористоть не равна просветности, то вводится структурный коэффициент , φ_α – в однородно пористой среде константа.

(3.6)

(3.7)

Учет структурного коэффициента приводит к уменьшению времени движения меченных частиц, т.к. .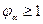

Еще одной важной характеристикой является средневзвешенное по объему порового пространства пластовое давление .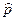

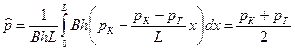
(3.8)

Таким образом, основные фильтрационные характеристики при прямолинейно-параллельной фильтрации несжимаемой жидкости определяются формулами (3.2, 3, 4, 6, 8)

Плоскорадиальная фильтрация несжимаемой жидкости

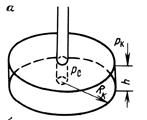
Схема плоскорадиального потока в круговом пласте.

Пусть имеем в круговом пласте толщиной h и радиуса R_к центральную скважину радиуса r_c, на забое которой поддерживается постоянное давление. На боковой поверхности r = R_к также поддерживается постоянное давление р_к (р_к > p_с) и через нее происходит приток флюида, равный дебиту скважины. Поэтому фильтрация установившаяся, а боковая поверхность, через которую происходит приток, называется контуром питания.

Выражение для дебита (объемного расхода) скважины

(3.9)

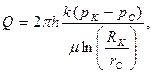
Равенство (3.9) называется формулой Дюпюи, по имени французского инженера-гидравлика XIX века.

Формулы для распределения давления в пласте

, (3.10)

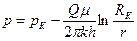
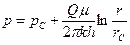
Или используя формулу Дюпюи равенства (3.10) можно привести к виду

, (3.11)

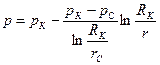
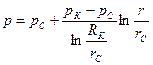
Скорость фильтрации определяется

(3.12)

Через любую цилиндрическую поверхность, концентрично расположенную относительно скважины, в единицу времени протекает один и тот же объем несжимаемой жидкости (Q = const). Поэтому вблизи контура питания площадь боковой поверхности цилиндра очень велика и скорости малы. При приближении скважине площадь поверхности постоянно уменьшается, и скорость возрастает (рис. 3.6). Для того чтобы скорость возрастала, необходимо увеличить градиент давления.

Уравнение индикаторной линии при плоскорадиальном потоке, также как и в случае фильтрации в галерее, задается уравнением прямой (рис. 3.7)

(3.13)

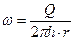
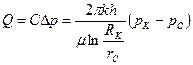
с коэффициентом продуктивности .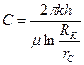

Вид индикаторной линии не зависит от геометрии потока и определяется только законом фильтрации. Отношение массового дебита скважины Qm к перепаду давления Dр называется коэффициентом продуктивности скважины С.

Из (3.13) для жидкости 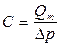или

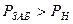
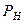
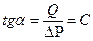
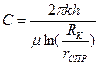
Коэффициент продуктивности определяется в результате исследования скважины при установившихся отборах. Если исследования скважины выполнены при (— давление насыщения нефти газом), то по тангенсу угла наклона коэффициент продуктивности скважины

, ,

где 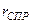— приведенный радиус скважины.

Приведенный радиус скважины – это радиус гидродинамически совершенной скважины, которая обеспечивает при равных прочих условиях такой же дебит, как гидродинамически несовершенная скважина, .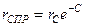

Расчетные соотношения для определения времени движения «меченой частицы» в плоскорадиальном потоке.

Если пористость равна просветностивремя движения «меченой частицы» от контура питания до произвольной точки пласта

или используя формулу Дюпюи (3.14)

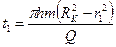
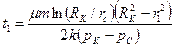
Из (3.14) следует, что «меченая частица» пройдет расстояние от контура питания до скважины за время Т

или r_C/R_K > 1

(3.17)

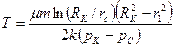
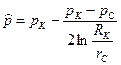
Радиально – сферическая фильтрация несжимаемой жидкости

Определим распределение давления и скорости фильтрации в изотропном недеформируемом пласте несжимаемой жидкости. Пусть имеется скважина радиуса r_C, вскрывшую кровлю пласта, на забое которой поддерживается постоянное давление р_С. Предположим, что толщина пласта h достаточно большая и можно выделить полусферу радиуса R_К на поверхности, которой поддерживается постоянное давление р_К и через нее проходит поток флюида, равный дебиту скважины. Течение установившееся, поверхность полусферы представляет собой контур питания. Тогда можно предположить, что вскрытие кровли пласта имеет форму полусферы и вектор скорости фильтрации в любой точке пласта между контуром питания и забоем скважины направлен к центру сферы. В этом случае задача имеет сферическую симметрию и ее удобнее решать в сферической системе координат.

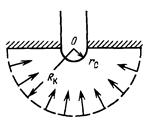
Формула распределения давления примет вид

(3.18)

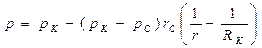
Формула для расчета дебита

(3.19)

.

Источник