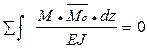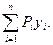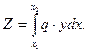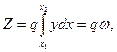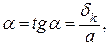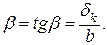что называется линией влияния

ЛИНИЯ ВЛИЯНИЯ

Смотреть что такое «ЛИНИЯ ВЛИЯНИЯ» в других словарях:

линия влияния — поверхность влияния Линия или поверхность, ординаты которой выражают значение какой либо величины (реакции, продольной или поперечной нагрузки, изгибающего момента, перемещения в данной точке системы и т. д.) в зависимости от положения… … Справочник технического переводчика

Линия влияния — – линия, координаты которой выражают значение усилий или перемещений в некоторой точке или элементе конструкции в зависимости от положения движущейся по конструкции сосредоточенной единичной силы постоянного направления. [Полякова, Т.Ю.… … Энциклопедия терминов, определений и пояснений строительных материалов

линия влияния — (инфлюэнта) (в строительной механике), график зависимости какой либо величины (усилия, прогиба и т. п.) в заданном сечении элемента конструкции от положения приложенной к нему единичной силы постоянного направления. Линии влияния применяются для… … Энциклопедический словарь

Линия влияния — линия, ординаты которой выражают значение усилий или перемещений в данной точке или элементе конструкции в зависимости от положения движущейся по конструкции сосредоточенной единичной силы постоянного направления. Источник: Справочник дорожных… … Строительный словарь

ЛИНИЯ ВЛИЯНИЯ — инфлюэнта, в строит. механике график зависимости к. л. величины (усилия, прогиба и т. п.) в заданном сечении элемента конструкции от положения приложенной к нему единичной силы пост. направления. Л. в. применяются гл. обр. для установления… … Большой энциклопедический политехнический словарь

линия влияния [поверхность влияния] — линия влияния поверхность влияния Линия или поверхность, ординаты которой выражают значение какой либо величины (изгибающего момента, перемещения в данной точке системы и т. д.) в зависимости от положения единичной силы постоянного направления.… … Справочник технического переводчика

Линии влияния поперечного воздействия нагрузки (линия влияния нагрузки) — поперечное сечение поверхности влияния усилий, характеризующее влияние жесткости поперечных связей пролетного строения на распределение временной нагрузки между главными балками. Источник: Справочник дорожных терминов … Строительный словарь

линия прямой видимости — Путь прямого (незагоризонтного) распространения радиоволн без учета их рефракции и влияния Земли. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики… … Справочник технического переводчика

Линия — В Викисловаре есть статья «линия» Линия (от лат. linea «льняная нить, шнур; линия») протяжённый и тонкий п … Википедия

Линия Специя-Римини — Романские языки в Европе. Линия Специя Римини представляет собой северную границу центрально итальянских диалектов (группа 17). Линия Рим Анкона отделяет южно срединно итальянские диалекты (группа 20) от южно итальянского ареала. Линия Специя… … Википедия

Источник

Понятие линии влияния. Использование линии влияния при расчете сооружений на подвижные нагрузки.

Линия влияния – это график, показывающий зависимость определяемой величины от по­ложения на сооружении единичного подвижного груза постоянного направления.

Линии влияния строятся двумя способами статическим и кинематическим.

При статическом методе используется статика, метод сечений. При построении линий влияния внутренних сил рассматривается положение груза слева и справа от расчетного сечения, соответственно получаем левые и правые линии влияния.

Сущность кинематического метода:

— отображается та связь, усилие в которой определяется. Получили механизм;

— взамен отброшенной связи прикладывается искомое усилие положительного направления;

— полученному механизму даем возможные перемещения в направлении искомого усилия;

— применяется принцип возможных перемещений: сумма работ всех действующих сил возможных перемещений равно нулю.

Определение усилий по линии влияния и заданной постоянной нагрузке.

1. Действие сосредоточенных сил Р.

S_к – определяемое усилие (R, Q, M); y_i – величина усилия S_к, когда единичный груз находится в сечении действия силы Р_i.

S_к = 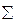P_i*y_i

2. Действие распределенной нагрузки q.

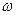
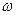
S_к = q* , где площадь линии влияния на участке действия равномерно распределенной нагрузки.

3. Действие сосредоточенного момента

S_к = М*tg

где 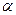– угол наклона линии влияния в том месте, где приложен момент и угол считается положительным при отсчете его от оси X до линии влияния против хода часовой стрелки.

Момент положителен по ходу часовой стрелки.

При одновременном действии всех нагрузок используется принцип независимости сил, все формулы объединяются:

S_к = 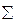P_i*y_i+ q* + М*tg .

6.Понятие ферм, признаки их статической неопределимости, определимости, основные способы определения усилий в стержнях ферм.

Расчёт плоских ферм.

Ферма- стержневая система, у которой во всех узлах шарнирыи при этом она остаётся геометрически неизменяемой.

Степень статической неопределимости ферм : n=C+Cо-2У,

где У-число узлов фермы.С-число стержней. Со-число опорных стержней.

Определение степени свободы для ферм:W=2У-С-Со.

Основные способы определения усилий в стержнях ферм:

1)Способ моментных точек

3)Способ вырезания узлов

-способ моментных точек:

СуммаМк1=-N1*r1-Ra*d+P1*d/2=0,отсюда находим N1.

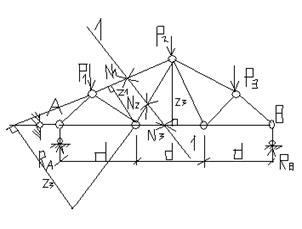
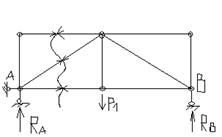
-способ проекций(моментные точки в бесконечности)

Статически неопределимые стержневые системы, определение степени статической неопр-ти, св-ва статически неопределимых систем. Сущность метода сил. Основные способы проверки правильности построения эпюр.

При расчете статически неопределимых рам определяют реакции опорных связей и внутренних усилий. Они принимаются за неизвестные. Если уравнений статики недостаточно для определения этих неизвестных, то система статически неопределима.

Свойства стат. неопределимых систем:

— распределение усилий между элементами зависит от материала этих элементов и их размеров;

— изменение температуры, смещение опорных связей, неточность изготовления элементов и последующей сборки все это приводит к появлению дополнительных усилий и напряжений.

Расчет статически неопределимых систем начинают с определения статической неопределимости – это число лишних связей, удаление которых превращает заданную стат. неопределимую раму в стат. определимую и геометрически неизменяемую.

Для рам степень статической неопределимости:

m – число замкнутых контуров в системе в предположении отсутствия шарнирных соединений;

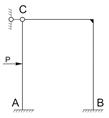
Задана стат. неопределимая рама. n=3*2 – 3 = 3 раза стат. неопределима.

Раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы.

Основная система метода сил – это статически определимая и геометрически неизменяемая система, полученная из заданной системы удалением лишних связей.

После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы обозначают Xi-, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы Xi, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

Эквивалентная система – это основная система, загруженная реакциями отброшенных связей и заданной нагрузкой. Она д. б. тождественна заданной раме статически (внутр. силы одинаковы) и кинематически (перемещение точек д. б. одинаковыми)

Теперь составим уравнения совместности перемещений:

_{1(x1,x2,x3,х4,Р)}=0

_{2(x1,x2,x3,х4,Р)}=0 – первый индекс направление перемещения, второй – причина перемещения

_{3(x1,x2,x3,х4,Р)}=0

_{4(x1,x2,x3,х4,Р)}=0

Применяем принцип независимости сил и их сложения:

_{1(x1,x2,x3,х4,Р)}= _{1(x1)+ 1(x2)+ 1(x3) + 1(x4) + 1(Р)}=0

_1(x1)= ₁₁*x₁ – принцип пропорциональности, где ₁₁ – перемещение по направлению x₁, от действия x₁=1; _1(x2)= ₁₂*x₂ и т. д.

Записываем канонические уравнения метода сил. Число уравнений равно степени статич. неопределимости. Каждое уравнение это отрицание перемещений по направлению отброшенных связей.

₁₁ x₁+ ₁₂ x₂+ ₁₃ x₃+ ₁₄ x₄+ _1(Р)=0 – канн. ур., отрицание перемещ. по направл. x₁.

₂₁ x₁+ ₂₂ x₂+ ₂₃ x₃+ ₂₄ x₄+ _2(Р)=0

₃₁ x₁+ ₃₂ x₂+ ₃₃ x₃+ ₃₄ x₄+ _3(Р)=0

₄₁ x₁+ ₄₂ x₂+ ₄₃ x₃+ ₄₄ x₄+ _4(Р)=0

Далее решаем каноническое уравнение. Для этого основную систему загружаем по отдельности единичными неизвестными по отдельности и строим эпюра единичных изгибаемых моментов. Находим коэффициенты при неизвестных:

_ik= ; _i(Р)=

Строим эпюру изгибающих моментов для заданной рамы:

М= 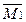Х₁+ Х₂+ Х₃+ Х₄+М_р

Способы проверки. Окончательная эпюра моментов проверяется дважды статически (явл. необходимой, но недостаточной) и кинематически.

Статическая – любой узел рамы должен находиться в равновесии, т. е. сумма моментов любого узла =0.

Кинематическая – проверяется отсутствие перемещений по направлению неизвестных (отброшенных связей). Сколько неизвестных столько и проверок:

₁= ; ₂=

Можно сделать суммарную проверку, т.е. отсутствие перемещений по направлению сразу всех неизвестных:

=М₁+ М₁+ М₂+ М₃; =

Источник

Понятие о линии влияния.

Решая статическую задачу, пренебрегают динамическим действием нагрузки, т.е.- исключают силы инерции, которые возбуждаются при вибрации самой балки и подвижного груза и не учитывают скорость движения груза. В динамике сооружений строятся динамические линии влияния, которые отражают наличие распределенных сил инерции сооружения и влияние скорости движения нагрузки.

Перейдем к получению статических линий влияния, применяя в каждый данный момент времени условия статического равновесия

Применяя принцип независимости изучают сначала действие лишь одного груза Р= 1, после чего легко получить значение усилия от груза поезда Р 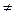1, увеличивая усилие от единичного груза в Р раз.

Линией влияния какого-либо усилия для определенного сечения сооружения называется графическое изображение закона изменения данного усилия в этом сечении при перемещении груза Р= 1 по длине сооружения.

Линия влияния представляет собой диаграмму, при построении которой функцией является изучаемая величина усилия, а независимой переменной — абсцисса груза Р= 1. Каждая ордината линии влияния численно равна значению изучаемого усилия для положения груза на сооружении над этой ординатой.

При построении линии влияния сечение неподвижно, положение груза меняется; при построении эпюры моментов меняется положение сечения, нагрузка неподвижна.

Рисунок 1.6.2 Рисунок 1.6.3

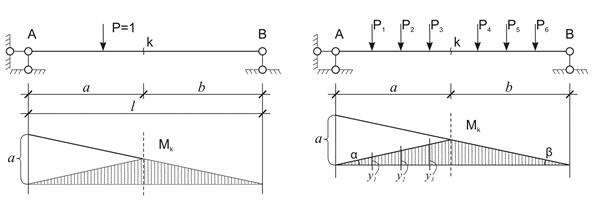
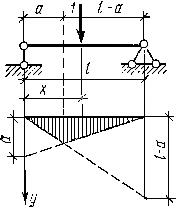
Нетрудно построить линии влияния усилий в простых статически определимых балках. Например, линию влияния изгибающего момента в сечении, расположенном на расстоянии а от левой опоры однопролетной балки, изображает график функции:

М_а=(l—а)х/l при 0 x): М_а = R_b(l-а). Линия влияния здесь имеет вид треугольника с вершиной в заданном сечении а. Максимальная ордината линии влияния при х= а

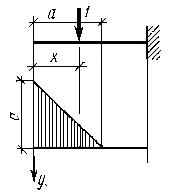
Линия влияния изгибающего момента в консольной балке (рисунок 1.6.3) для сечения, находящегося на расстоянии а от свободного конца, выражается формулами

Легко построить также линии влияния поперечной силы в произвольной точке, находящейся на расстоянии а от левого конца однопролетной или консольной балки. Эти линии влияния выражаются уравнениями:

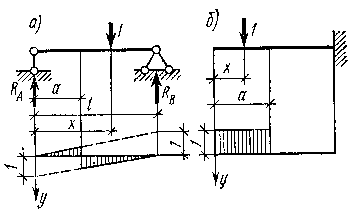
для однопролетной балки (рис. 1.6.4, а)

для консольной балки (рис. 1.6, 6)

При х = а линии влияния поперечных сил имеют разрыв на величину, равную единице.

Несколько сложнее построение линий влияния усилий в элементах статически определимых форм, арок и других систем. Еще более сложными методами строятся линии влияния и элементах статически неопределимых систем. В общем случае ординаты линий влияния можно вычислить по точкам, прилагая каждый раз единичную силу в соответствующей точке и определяя рассматриваемое усилие обычным расчетом. Заметим, что линии влияния усилий в статически определимых системах при движении груза по прямой изображаются отрезками прямых линий, в то время как линии влияния усилий в статически неопределимых системах, как правило, криволинейные.

Дата добавления: 2016-01-18 ; просмотров: 1320 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Общая теории линий влияния

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Рязанский институт (филиал)

Государственного образовательного учреждения

Высшего профессионального образования

«Московский государственный открытый университет»

В. А. Долгоруков, Г. С. Нечипорук

Статически определимые

Стержневые системы

В примерах

Методические указания для

Студентов строительных специальностей

Рязань

В. А. Долгоруков, Г. С. Нечипорук.

Статически определимые стержневые системы в примерах. Методические указания для студентов строительных специальностей. Рязанский институт (филиал) Государственного образовательного учреждения «Московский государственный открытый университет», 2010

В методических указаниях даны необходимые сведения о методах расчета статически определимых стержневых систем (многопролетных балок, ферм, арок и рам) на неподвижную и подвижную нагрузки и приведены примеры по определению внутренних усилий и перемещений. Даны схемы и исходные данные для выполнения расчетно-графических работ.

Печатается по решению методического совета вуза

© Рязанский институт (филиал) МГОУ, 2010

Оглавление

1.Статически определимые многопролетные балки………………………………4

1.1. Общая теория линий влияния…………………………………………………..4

1.2. Расчет статически определимых многопролетных балок на

неподвижную и подвижную нагрузки……………………………………….…. 13

2. Статически определимые фермы……….……..………………..…………..….25

2.1. Расчет простейших ферм на неподвижную нагрузку……………………….26

2.2. Расчет ферм на подвижную нагрузку…………………………………….…..32

3. Статически определимые арки…….. ………………………………………. 36

3.1 Аналитический расчет трехшарнирной арки………………………………. 37

3.2 Расчет арок на подвижную нагрузку………………………………………… 47

4. Расчет на прочность и жесткость ломаных стержней…………… …………. 57

4.1 Построение эпюр внутренних усилий в раме………………………………. 57

4.2 Определение перемещений в стержневых системах методом Мора………61

5.Список рекомендуемой литературы…. ……………………….……………….73

Задание к расчетно-графической работе № 1 (многопролетная балка )………..75

Задание к расчетно-графической работе № 2 (статически определимая ферма)77

Задание к расчетно-графической работе № 3 (трехшарнирная арка, рама)……81

Задание к контрольной работе (статически определимая рама)……………..….85

Статически определимые многопролетные балки

Общая теории линий влияния

1.1.1 Понятие о линиях влияния

При расчете мостов, кранов и других инженерных сооружений часто приходится иметь дело с подвижной нагрузкой различного вида. Обычно подвижная нагрузка состоит из системы параллельных друг другу (чаще вертикальных) грузов, между которыми сохраняется неизменное положение. Примерами такой нагрузки являются поезд, перемещающийся по железнодорожному мосту, кран, движущийся по подкрановой балке, и др.

Усилия в том или ином элементе сооружения (а также его деформации) зависят от положения подвижной нагрузки. Для определения расчетных величин усилий необходимо из всех возможных положений нагрузки выбрать такое, при котором рассчитываемый элемент будет находиться в наиболее неблагоприятных условиях. Такое положение нагрузки называется невыгоднейшим, или опасным.

Указанные выше задачи позволяют решать линии влияния(л. в.). Линия влияния это график, выражающий изменение той или иной величины (опорной реакции, внутреннего усилия, перемещения в заданном сечении и т. п.) от положения движущегося по сооружению единичного груза постоянного направления.

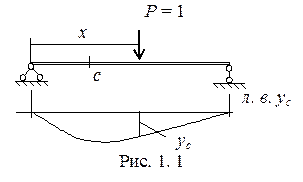На рис. 1. 1 для примера показана линия влияния прогиба в сечении «с» при перемещении силы Р = 1 по сооружению.

Линию влияния необходимо отличать от эпюры. Это противоположные друг другу понятия. Действительно, ординаты эпюры характеризуют распределение изучаемого фактора (например изгибающего момента) по различным сечениям балки при неподвижной нагрузке; ординаты линии влияния, наоборот, характеризуют изменение фактора (например того же момента), возникающего в одном определенном сечении при перемещающейся по длине балки силы Р = 1.

Зная линию влияния какой-либо искомой величины нетрудно определить ее значение при действии системы сосредоточенных грузов, распределенной нагрузки или сосредоточенного момента.

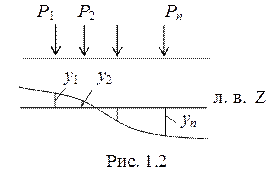а) Влияние системы сосредоточенных грузов (рис. 1. 2). Пусть имеем систему сосредоточенных грузов Р₁, Р₂,…. Р_n. Требуется определить влияние этой нагрузки на величину Z, для которой известна линия влияния. Влияние каждой из сил выражается произведением P_i∙y_i. Пользуясь принципом независимости действия сил можем записать

Z = P₁∙y₁ + P₂∙y₂ +……+ P_n∙y_n =

б) Влияние сосредоточенного момента M (рис. 1. 3). Любой момент можно заменить парой сил, расположенных на плече h. Тогда его влияние можно оценить по следующей формуле

где φ – угол наклона касательной к линии влияния Z в точке приложения М.

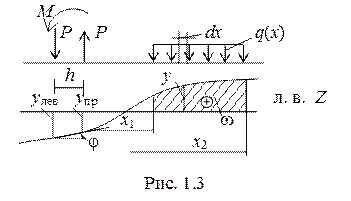в) Влияние распределенной нагрузки (рис. 1. 3). Элементарная сила q∙dx будет вызывать элементарное усилие dZ = q∙dx∙y. Тогда полное усилие Z определится как

В случае равномерной нагрузки при q = const

где ω – площадь линии влияния Z под распределенной нагрузкой q.

1.1.2 Построение линий влияния в простой балке

Построение линий влияния опорных реакций.

Для построения линии влияния какого-либо параметра необходимо получить формулу (выражение) этого параметра.

Запишем выражение для реакции R_a

или

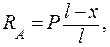
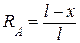
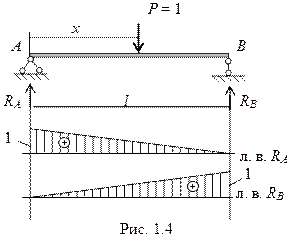
л. в. . (1.1)

Линия влияния реакции R_a показана на рис. 1.4.

Для построения л.в. R_В запишем выражение этой реакции.

SM_А = 0. R_Вl – P∙ x = 0. 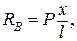или

л. в. 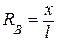. (1.2)

При х = 0 R_В = 0, при х = l R_В = 1. Линия влияния реакции R_В показана на рис. 1.4.

Построение линий влияния внутренних усилий.

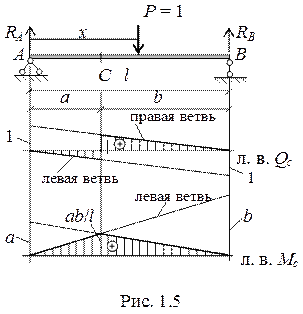
Построение линий влияния Q_c.

Пусть единичная сила находится справа от сечения «с» (рис. 1.5). Тогда, рассматривая левую от сечения часть балки, можем записать Q_c = R_a, или

Теперь Р = 1 перемещается слева от сечения «с». Рассмотрим правую часть балки.

Получили уравнение левой ветви. В соответствии с полученными уравнениями (1.3) и (1.4) строим линию влияния Q_c (рис. 1.5).

Для построения линии влияния изгибающего момента в сечении «С» используем ту же методику, что и при построении л. в. Q_c.

Пусть Р = 1 перемещается справа от сечения «С». Рассмотрим левую часть балки. Изгибающий момент в сечении «С» будет

Таким образом, правая ветвь линии влияния повторяет линию влияния R_a, с множителем «а» (рис. 1.5).

Теперь Р = 1 перемещается слева от сечения «С». Рассмотрим правую часть балки, тогда

Линия влияния М_c приведена на рис. 1.5.

Отметим, что при построении линий влияния положительные ординаты откладывают выше оси ординат. Линии влияния реакций и поперечных сил безразмерны, поскольку величина единичной силы безразмерна, линии влияния моментов имеют размерность «метр».

Линии влияния для консольной балки

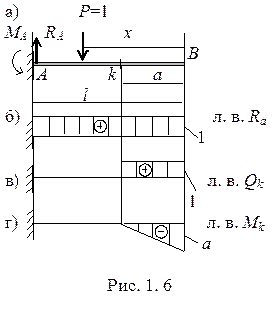Линия влияния реакции R_a

Из уравнения равновесия S y = 0, получим R_a = P = 1, т. е.

Линия влияния поперечной силы в сечении «k» Q_k.

Единичная сила Р = 1 находится справа от сечения «k». Рассмотрим правую часть балки.

Далее, Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки.

Линия влияния изгибающего момента в сечении «k» М_k.

Пусть Р = 1 справа от сечения «k». Рассмотрим правую часть балки.

Теперь Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки.

Линии влияния Q_k и М_k приведены на рис. 1. 6 (в, г).

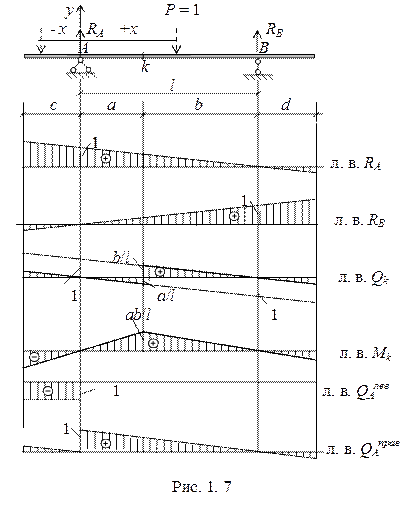
Пример 1.1. Построить линии влияния реакций и Q_k и М_k в шарнирно опертой балке с консолями (рис. 1.7.).

Решение. Если выбрать начало координат на левой опоре в точке А, то полученные выше выражения для линий влияния в простой балке справедливы и в данном случае. При этом, координата х будет меняться от – с до l + d.

Дополнительно необходимо построить линии влияния поперечной силы для двух соседних сечений – одно слева от опоры А, другое справа от той же опоры.

1.1.3 Построение линий влияния при узловой передаче нагрузки.

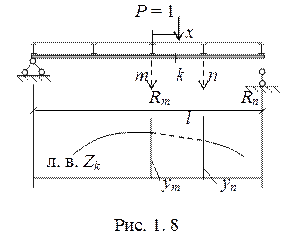
Часто нагрузка передается на конструкцию не непосредственно, а через систему статически определимых балок (настилов) (рис. 1.8). Когда единичный груз находится в начале (т. m) или в конце балки (т. n) то он полностью передается на основную конструкцию и вызывает усилия или y_m,или y_n.

При движении единичной силы внутри вспомогательной балки ее действие на конструкцию осуществляется через опорные реакции R_m и R_n. Общее влияние в этом случае можно записать как:

В свою очередь сами реакции равны (они определяются как в обычной балке)

Тогда

—

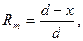
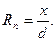
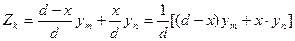
получили уравнение прямой. При х = 0 Z_k = y_m, при x = d Z_k = y_n. Прямая, соединяющая ординаты y_m и y_n называется передаточная прямая.

В качестве примера на рис. 1.9 показаны линии влияния при узловой передаче нагрузки в пролетном строении моста.

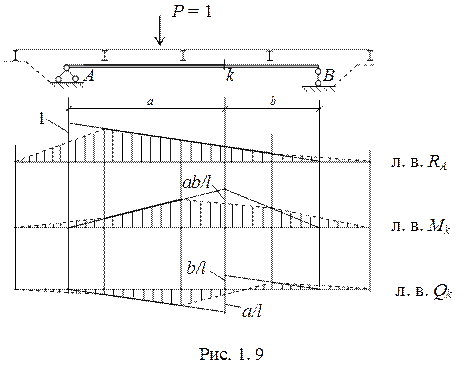1.1.4 Кинематический метод построения линий влияния

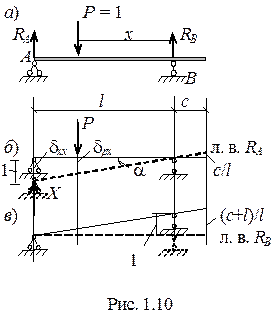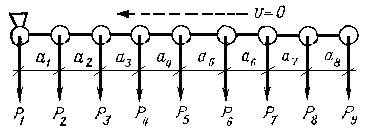
На основании этого принципа можно записать (рис. 1.10, б)

d_xx – постоянная величина,

d_px – переменная, зависит от х, следовательно

d_px = х∙tga, d_xx= l∙tga, тогда 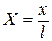, т. е. линия влияния левой реакции R_А повторяет эпюру перемещений балки при смещении левой опоры на единицу.

Аналогично получаем линию влияния R_В (рис. 1.10, в) путем вертикального смещения опоры B на единицу.

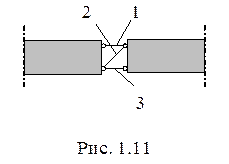При построении линий влияния Q и М необходимо убрать связи, воспринимающие соответственно поперечную силу и изгибающий момент. Известно, что для соединения в неподвижную систему двух дисков (стержней) достаточно трех связей (рис.1.11). Если убрать 2-ю связь, то данное сечение не будет воспринимать поперечную силу, а вертикальные кромки (торцы) левого и правого стержней будут смещаться параллельно друг другу.

Для построения линии влияния поперечной силы в сечении k Q_k двухопорной балки (рис. 1.12) убираем 2-ю связь и даем торцам взаимное вертикальное смещение на единицу, приложив в районе торцов малые положительные поперечные силы (рис. 1.12, б). Отметим, что если при взаимном смещении торцы стержней параллельны, то параллельны друг другу левый и правый стержни целиком. На рис. 1.12, в показан вид линии влияния Q_k.

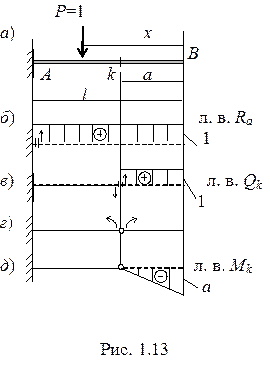Если убрать в рассматриваемом сечении (рис. 1.11) 1-ю или 3-ю связь, то жесткое соединение превратится в шарнирное, поскольку в этом случае торцы могут свободно поворачиваться относительно друг друга. Такое сечение не воспринимает изгибающий момент. Врезав в сечении k шарнир (рис. 1.12, г) и задав единичное угловое смещение, приложив малые положительные моменты, можем записать работу сил на возможных перемещениях

Так как a и b малы, можем записать:

Таким образом, эпюры возможных перемещений, дают вид линии влияния М_k (рис. 1.12, д).

Для консольной балки линии влияния, полученные кинематическим способом, имеют вид, показанный на рис 1.13.

1.2 Расчет статически определимых многопролетных балок на

Источник