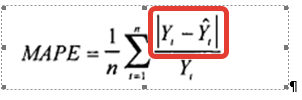средняя абсолютная ошибка что показывает
Методы оценки качества прогноза
Часто при составлении любого прогноза — забывают про способы оценки его результатов. Потому как часто бывает, прогноз есть, а сравнение его с фактом отсутствует. Еще больше ошибок случается, когда существуют две (или больше) модели и не всегда очевидно — какая из них лучше, точнее. Как правило одной цифрой (R 2 ) сложно обойтись. Как если бы вам сказали — этот парень ходит в синей футболке. И вам сразу все стало про него ясно )
Остатки
Суровые MSE и R 2
Когда нам требуется подогнать кривую под наши данные, то точность этой подгонки будет оцениваться программой по среднеквадратической ошибке (mean squared error, MSE). Рассчитывается по незамысловатой формуле 
где n-количество наблюдений.
Соотвественно, программа, рассчитывая кривую подгонки, стремится минимизировать этот коэффициент. Квадраты остатков в числителе взяты именно по той причине, чтобы плюсы и минусы не взаимоуничтожились. Физического смысла MSE не имеет, но чем ближе к нулю, тем модель лучше.
Вторая абстрактная величина это R 2 — коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. В отличии от MSE не зависит от единиц измерения данных, поэтому поддается сравнению. Рассчитывается коэффициент по следующей формуле: 
где Var(Y) — дисперсия исходных данных.
Безусловно коэффициент детерминации — важный критерий выбора модели. И если модель плохо коррелирует с исходными данными, она вряд ли будет иметь высокую предсказательную силу.
MAPE и MAD для сравнения моделей
Среднее абсолютное отклонение (mean absolute deviation, MAD) определяется как частное от суммы остатков по модулю к числу наблюдений. То есть, средний остаток по модулю. Удобно? Вроде да, а вроде и не очень. В моем примере MAD=43. Выраженный в абсолютных единицах MAD показывает насколько единиц в среднем будет ошибаться прогноз.
MAPE призван придать модели еще более наглядный смысл. Расшифровывается выражение как средняя абсолютная ошибка в процентах (mean percentage absolute error, MAPE). 
где Y — значение исходного ряда.
Выражается MAPE в процентах, и в моем случае означает, что в модель может ошибаться в среднем на 16%. Что, согласитесь, вполне допустимо.
Наконец, последняя абсолютно синтетическая величина — это Bias, или просто смещение. Дело в том, что в реальном мире отклонения в одну сторону зачастую гораздо болезненнее, чем в другую. К примеру, при условно неограниченных складских помещениях, важнее учитывать скачки реального спроса вверх от спрогнозированных значений. Поэтому случаи, где остатки положительные относятся к общему числу наблюдений. В моем случае 44% спрогнозированных значений оказались ниже исходных. И можно пожертвовать другими критериями оценки, чтобы минимизировать этот Bias.
Можете попробовать это сами в 

Интересно узнать — какие методы оценки качества прогнозирования вы используете в своей работе?
СОДЕРЖАНИЕ
MAPE в задачах регрессии
Средняя абсолютная процентная ошибка обычно используется в качестве функции потерь для задач регрессии и при оценке модели из-за ее очень интуитивной интерпретации с точки зрения относительной ошибки.
Определение
Как следствие, использование MAPE очень просто на практике, например, с использованием существующих библиотек для квантильной регрессии, позволяющей использовать веса.
Последовательность
Использование MAPE в качестве функции потерь для регрессионного анализа возможно как с практической, так и с теоретической точки зрения, поскольку можно доказать существование оптимальной модели и согласованность минимизации эмпирического риска.
Альтернативные определения
Проблемы могут возникнуть при вычислении значения MAPE с рядом малых знаменателей. Может возникнуть проблема сингулярности в форме «единица, деленная на ноль» и / или создание очень больших изменений абсолютной процентной ошибки, вызванных небольшим отклонением в ошибке.
В качестве альтернативы каждое фактическое значение ( A t ) ряда в исходной формуле может быть заменено средним значением всех фактических значений ( Ā t ) этого ряда. Эта альтернатива все еще используется для измерения эффективности моделей, прогнозирующих спотовые цены на электроэнергию.
Проблемы
Хотя концепция MAPE звучит очень просто и убедительно, у нее есть серьезные недостатки в практическом применении, и существует множество исследований недостатков и вводящих в заблуждение результатов MAPE.
Чтобы преодолеть эти проблемы с MAPE, в литературе предлагаются некоторые другие меры:
Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
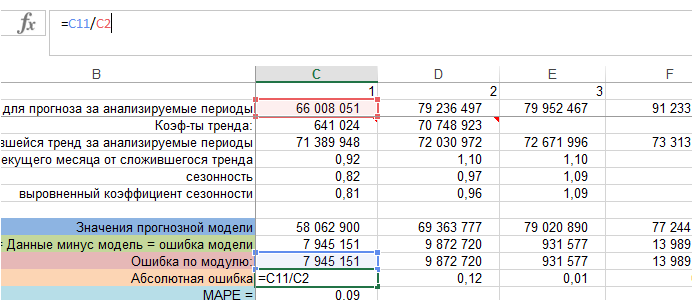
 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется:
В данной статье мы рассмотрим, как рассчитать MAPE в Excel и как ее использовать.
Формула расчета MAPE:
Для того, чтобы рассчитать среднюю абсолютную ошибку мы:
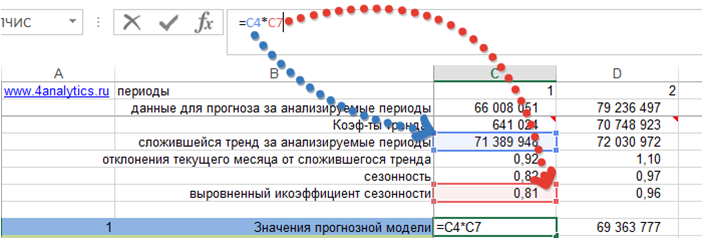
1. Рассчитаем значение модели прогноза — Ŷt
Возьмем модель с трендом и сезонностью. Рассчитаем значение модели для каждого периода, когда нам известны фактические продажи. Для этого сложившийся тренд за анализируемый период умножим на коэффициент сезонности для соответствующего месяца.
Получили значения прогнозной модели для каждого периода времени:
Подробнее о расчете прогноза с помощью тренда и сезонности читайте в статье «Расчет прогноза с помощью тренда и сезонности».
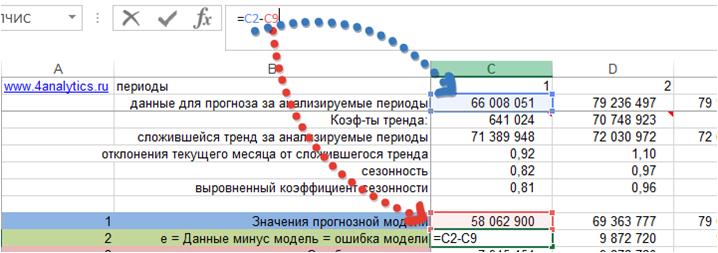
2. Рассчитаем значения ошибки прогноза.
В формуле расчета MAPE – это:
Получили значение ошибки прогноза для каждого момента времени за анализируемый период.
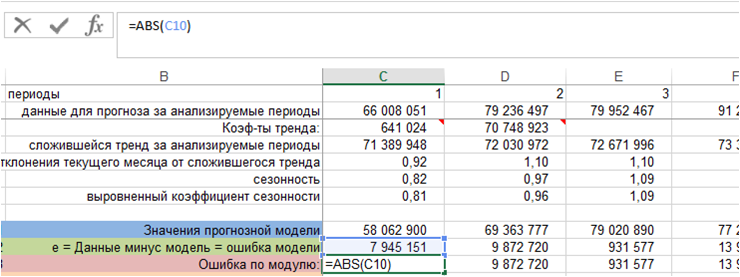
3. Рассчитаем ошибку по модулю.
Для этого воспользуемся функцией Excel =ABC()
4. Определяем абсолютную ошибку.
Для каждого периода ошибку по модулю делим на фактические значения ряда, т.е. на фактический объем продаж:
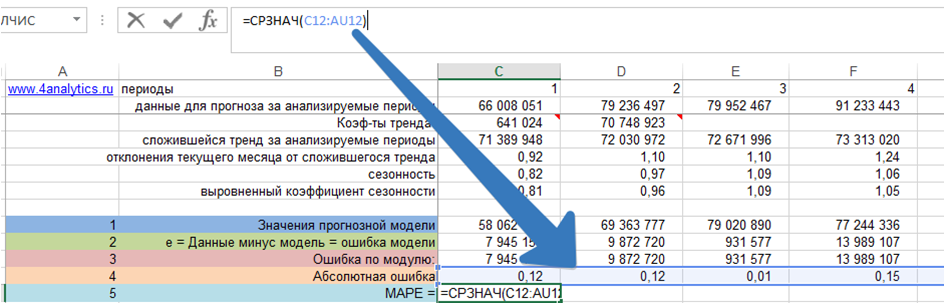
5. Рассчитаем MAPE – среднюю абсолютную ошибку.
Для этого рассчитаем среднее значение абсолютной ошибки за все периоды:
Как рассчитать показатель точность прогноза?
Показатель точность прогноза = 1 –MAPE:
С помощью MAPE вы можете сравнивать различные модели между собой, можете оценивать, как и на сколько модель делает точные прогнозы для разных временных рядов.
А также, что самое главное, можете оценить экономический эффект для компании за счет повышения точности прогноза.
Если есть вопросы, пожалуйста, пишите в комментариях!
Forecast4AC PRO рассчитает MAPE для каждого временного ряда!
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
Тестируйте возможности платных решений:
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
В статистика, средняя абсолютная ошибка (MAE) является мерой ошибки между парными наблюдениями, выражающими одно и то же явление. Примеры Y против Икс включают сравнения прогнозируемого и наблюдаемого, последующего времени и начального времени, а также один метод измерения по сравнению с альтернативным методом измерения. MAE рассчитывается как:
Содержание
Несогласие по количеству и разногласию по распределению
Связанные меры
Если модель прогнозирования должна быть адаптирована с использованием выбранной меры производительности в том смысле, что наименьших квадратов подход связан с среднеквадратичная ошибка, эквивалент средней абсолютной ошибки равен наименьшие абсолютные отклонения.
Свойство оптимальности
В средняя абсолютная ошибка реальной переменной c с уважением к случайная переменная Икс является
При условии, что распределение вероятностей Икс такова, что указанное выше ожидание существует, то м это медиана из Икс если и только если м является минимизатором средней абсолютной ошибки относительно Икс. [6] Особенно, м является выборочной медианой тогда и только тогда, когда м минимизирует среднее арифметическое абсолютных отклонений. [7]
В более общем смысле медиана определяется как минимум
Это основанное на оптимизации определение медианы полезно при статистическом анализе данных, например, в kкластеризация медианы.
Доказательство оптимальности
Дифференциация по а дает








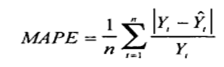 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется: