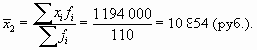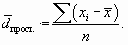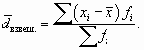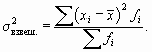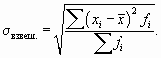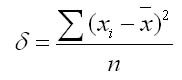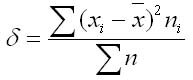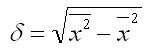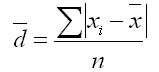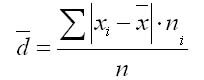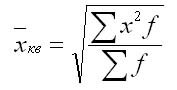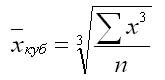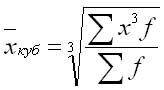среднее линейное отклонение в статистике что показывает
Понятие вариации. Расчет среднего линейного отклонения
Поможем написать любую работу на аналогичную тему
Различие в индивидуальных значениях признака внутри изучаемой совокупности в статистике называется вариацией признака.
Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае.
Средняя величина ¾ это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены они вблизи или значительно отклоняются от нее.
В тех случаях, когда отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются, средняя хорошо представляет всю совокупность. В тех же случаях, когда отдельные значения совокупности далеко отстают от средней, средняя плохо представляет всю совокупность.
Колеблемость отдельных значений характеризуют показатели вариации.
Термин «вариация» произошел от латинского variatio ¾ изменение, колеблемость, различие. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием различных факторов. Различают случайную и систематическую вариации признака.
Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих его факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а, следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц хi к средней измеряется рядом абсолютных, средних и относительных показателей.
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним.
Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них ¾ размах вариации.
Размах вариации (R) ¾ это разность между наибольшим (хmax) и наименьшим (хmin) значениями вариантов:
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариантов в ряду.
Для того чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как средняя арифметическая отклонений индивидуальных значений от средней без учета знака этих отклонений:
Порядок расчета среднего линейного отклонения следующий:
1) по значениям признака исчисляется средняя арифметическая:
2) определяются отклонения каждого варианта хi от средней:
3) рассчитывается сумма абсолютных величин отклонений:
4) сумма абсолютных величин отклонений делится на число значений:
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:
Порядок расчета среднего линейного отклонения взвешенного следующий:
1) вычисляется средняя арифметическая взвешенная:
2) определяются абсолютные отклонения вариантов от средней:
3) полученные отклонения умножаются на частоты:
4) находится сумма взвешенных отклонений без учета знака:
5) сумма взвешенных отклонений делится на сумму частот:
Показатели вариации в статистике
7.1. Абсолютные и относительные показатели вариации
Рассмотрим две совокупности сотрудников рекламных агентств.
Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., fi | xi*fi |
|---|---|---|---|
| 4 000-6 000 | 5 000 | 10 | 50 000 |
| 6 000-8 000 | 7 000 | 6 | 42 000 |
| 8 000-10 000 | 9 000 | 19 | 171 000 |
| 10 000-12 000 | 11 000 | 26 | 286 000 |
| 14 000-16 000 | 15 000 | 10 | 150 000 |
| 16 000-18 000 | 17 000 | 5 | 85 000 |
| Сумма | — | 95 | 1 031 000 |
Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., fi | xi*fi |
|---|---|---|---|
| 1 500-4 500 | 3 000 | 9 | 27 000 |
| 4 500-7 500 | 6 000 | 26 | 156 000 |
| 7 500-10 500 | 9 000 | 24 | 216 000 |
| 10 500-13 500 | 12 000 | 18 | 216 000 |
| 13 500-16 500 | 15 000 | 14 | 210 000 |
| 16 500-19 500 | 18 000 | 10 | 180 000 |
| 19 500-22 500 | 21 000 | 9 | 189 000 |
| Сумма | — | 110 | 1 194 000 |
Рассчитаем средний уровень заработной платы:
Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.
Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.
Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака
 | ( 7.1) |
Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение
 | ( 7.2) |
Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:
 | ( 7.3) |
Дисперсией (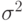
) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней
 | ( 7.4) |
 | ( 7.5) |
Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением):
 | ( 7.6) |
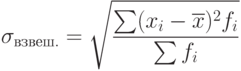 | ( 7.7) |
Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:
Среднее линейное и среднее квадратическое отклонение
Среднее квадратическое отклонение
Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:
1. Для первичного ряда:
2. Для вариационного ряда:
Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:
Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.
Примеры нахождения cреднего квадратического отклонения: Пример 1, Пример 2
Для альтернативных признаков формула среднего квадратичного отклонения выглядит так:
где р — доля единиц в совокупности, обладающих определенным признаком;
q — доля единиц, не обладающих этим признаком.
Понятие среднего линейного отклонения
Среднее линейное отклонение определяется как средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средних арифметических.
1. Для первичного ряда:
2. Для вариационного ряда:
где сумма n — сумма частот вариационного ряда.
Пример нахождения cреднего линейного отклонения: Пример 1
Преимущество среднего абсолютного отклонения как меры рассеивания перед размахом вариации, очевидно, так как эта мера основана на учете всех возможных отклонений. Но этот показатель имеет существенные недостатки. Произвольные отбрасывания алгебраических знаков отклонений могут привести к тому, что математические свойства этого показателя являются далеко не элементарными. Это сильно затрудняет использование среднего абсолютного отклонения при решении задач, связанных с вероятностными расчетами.
Поэтому среднее линейное отклонение как мера вариации признака применяется в статистической практике редко, а именно тогда, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется оборот внешней торговли, состав работающих, ритмичность производства и т. д.
Среднее квадратическое
Среднее квадратическое применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.
Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.
Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
Средняя квадратичная взвешенная вычисляется по формуле:
где f — признак веса.
Средняя кубическая
Средняя кубическая применяется, например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:
Средняя кубическая взвешенная:
При расчете средних величин и дисперсии в интервальных рядах распределения истинные значения признака заменяются центральными значениями интервалов, которые отличны от средней арифметической значений, включенных в интервал. Это приводит к возникновению систематической погрешности при расчете дисперсии. В.Ф. Шеппард определил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала как в сторону повышения, так и в сторону понижения величины дисперсии.
Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по значительному количеству исходных данных (n > 500). Однако исходя из того, что в ряде случаев обе погрешности, действуя в разных направлениях компенсируют друг друга, можно иногда отказаться от введения поправок.
Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина.
В практике статистики часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для таких сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.
Для осуществления таких сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с разными средним арифметическим используется относительный показатель вариации — коэффициент вариации.
Структурные средние
Для характеристики центральной тенденции в статистических распределениях не редко рационально вместе со средней арифметической использовать некоторое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.
Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.
Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Показатели вариации признака (среднее линейное отклонение, дисперсия простая и взвешенная), среднее квадратическое отклонение.
Поможем написать любую работу на аналогичную тему
Средняя величина не раскрывает строения совокупности, она не показывает, как располагаются около нее варианты осредняемого признака. Исследование вариации в статистике дает возможность оценить степень воздействия на признак других варьирующих признаков. Вариация — это различие в значениях какого-либо признака у различных единиц совокупности в один и тот же период времени. Вариация существует в пространстве — это колеблемость значений признака по отдельным территориям и во времени — изменение значений признака в различные периоды времени. Исследование вариации помогает познать сущность изучаемого явления.
Для измерения вариации признака в совокупности применяют ряд обобщающих показателей:
среднее линейное отклонение;
средний квадрат отклонений (дисперсия);
среднее квадратическое отклонение;
Наиболее простым измерителем вариации является разность между наибольшим и наименьшим значением признака и называется размах вариации и исчисляется по формуле:
где R — размах вариации;
Показатель вариации учитывает крайние значения признака, которые сильно могут отличаться от всех других единиц, поэтому иногда пользуются показателем осцилляции:
где K — коэффициент осцилляции;
R — размах вариации;
— средняя арифметическая этого ряда.
Среднее линейное отклонение представляет среднюю арифметическую из абсолютных значений отклонений отдельных вариаций (значений признака) от их средней арифметической (знаки отклонений не учитываются). Среднее линейное отклонение может быть простым и взвешенным и измеряется в тех же единицах, что и величина признака. Вычисление среднего линейного отклонения производится по формулам:
1. для несгруппированных данных:
где 
— среднее линейное отклонение;
x — значениe признака;
— среднее значение признака;
n — численность признаков.
2. если данные наблюдения представлены в виде дискретного ряда распределения с частотами, тогда:
Число повторений вариантов значений признака, называют частотой повторений. Если частоты представлены в относительных величинах, то их называют частостями.
Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от общей средней величины. исперсия еще называется средним квадратом отклонений и обозначается 
(сигма квадрат). В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
реднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается 
(сигма):
Среднее квадратическое отклонение — это обобщающая характеристика абсолютных размеров вариации признака в совокупности и выражается в тех же единицах измерения, что и сам признак (в метрах, тоннах, гектарах и т. д.). Вычислению среднего квадратического отклонения предшествует расчет дисперсии. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения.
В практике часто возникает необходимость сравнения вариаций различных признаков, например, вариаций возраста рабочих и их квалификации; стажа работы и производительности труда; себестоимости и прибыли и т. д.
Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют коэффициент вариации.
Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
%.
В отличие от среднего квадратического отклонения коэффициент вариации является относительной величиной, что используется при сравнении вариаций любых совокупностей.
По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее явление. И чем больше его величина (V), тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.