среднее или медиана что лучше
Блог об аналитике, визуализации данных, data science и BI
Дашборд первых 8 месяцев жизни малыша
Анализ рынка вакансий аналитики и BI: дашборд в Tableau
Анализ альбомов Земфиры: дашборд в Tableau
Гайд по современным BI-системам
Различия между медианой и средним арифметическим как целевым показателем анализа данных
В сегодняшней статье мы бы хотели осветить простую, но в то же время важную тему выбора простой метрики для оценки того или иного датасета. Со средним арифметическим все давным давно знакомы, чуть ли не каждый школьник отлично знает, что нужно просуммировать все имеющиеся значения, поделить на их количество и получить среднее значение. В школьные знания не входят никакие альтернативные варианты, которых, на самом деле, в статистике много — на любой вкус и случай. Однако, в решении исследовательских и маркетинговых задач люди часто берут именно эту метрику за основу. Правомерно ли это или есть более удачный вариант? Давайте разбираться.
Для начала стоит вспомнить определения двух метрик, о которых мы сегодня поговорим.
Среднее — самый популярный статистический показатель, который используется для измерения центра данных. А что же такое медиана? Медиана — значение, которое разбивает данные, отсортированные по порядку увеличения значений, на две равные части. Это значит, что медиана показывает центральное значение в выборке, если наблюдений нечетное количество и среднее арифметическое двух значений, если количество наблюдений в выборке четно.
Исследовательские задачи
Итак, оценка среднего значения выборки — зачастую важна во многих исследовательских вопросах. Например, специалисты, изучающие демографию часто задаются вопросом изменения численности регионов России, чтобы проследить за динамикой и отразить это в отчетностях. Давайте попробуем рассчитать среднюю численность региона России, а также медиану, а затем сравним полученные результаты.
Для начала, нужно найти и загрузить данные, подключив для этого библиотеку pandas.
Затем, нужно посчитать среднее и медиану выборки.
Значения, естественно, получились разными, так как распределение наблюдений в выборке отлично от нормального. Для того, чтобы понять, сильно ли они отличаются, построим график распределения и отметим среднее и медиану.
Также, на этих данных стоит построить боксплот для более точной визуализации основных квантилей распределения, медианы, среднего и выбросов.
Из графиков следует, что медиана существенно меньше среднего, а также, ясно, что это следствие наличия больших выбросов — Москвы и Санкт-Петербурга. Поскольку среднее арифметическое — метрика крайне чувствительная к выбросам — при их наличии в выборке опираться на выводы относительно среднего не стоит. Рост или снижение численности населения Москвы может сильно смещать среднюю численность по России, однако это не будет влиять на настоящий общерегиональный тренд.
Используя среднее арифметическое мы скажем, что численность типичного (среднего) города в РФ — 268 тысяч человек. Однако, это вводит нас в заблуждение, так как среднее значительно превышает медиану исключительно из-за численности населения Москвы и Санкт-Петербурга. На самом деле, численность типичного российского города существенно меньше (аж в 2 раза!) и составляет 104 тысячи жителей.
Маркетинговые задачи
В контексте бизнеса разница между средним арифметическим и медианой также важна, так как использование неверной метрики может серьезно сказаться на результатах проведения акции или затруднить достижение цели. Давайте посмотрим на реальном примере, с какими трудностями может столкнуться предприниматель в ритейле, если неверно выберет целевую метрику.
Для начала, как и в предыдущем примере, загрузим датасет о покупках в супермаркете. Выберем необходимые для анализа столбцы датасета и переименуем их, для упрощения кода в дальнейшем. Поскольку эти данные не так хорошо подготовлены, как предыдущие, необходимо сгруппировать все купленные товары по чекам. В этом случае необходима группировка по двум переменным: по id покупателя и по дате покупки (дата и время определяется моментом закрытия чека, поэтому все покупки в рамках одного чека совпадают по дате). Затем, назовем полученный столбец «total_bill», то есть сумма чека и посчитаем среднее и медиану.
Теперь, как и в предыдущем примере нужно построить график распределения чеков покупателей и боксплот, а также отметить медиану и среднее арифметическое на каждом из них.
Из графиков следует, что распределение смещено к началу координат (отличное от нормального), а значит медиана и среднее не равны. Медианное значение меньше среднего примерно на 220 рублей.
Теперь представим, что у маркетологов есть задача повысить средний чек покупателя. Маркетолог может решить, что поскольку средний чек равен 601 рублю, то можно предложить следующую акцию: «Всем покупателям, кто совершит покупку на 600 рублей, мы предоставляем скидку 20% на товар за 100 рублей». В целом, резонное предложение, однако, в реальности, средний чек ниже — 378 рублей. То есть большая часть покупателей не заинтересуется в предложении, поскольку их покупка обычно не достигает предложенного порога. Это значит. что они не воспользуются предложением и не получат скидку, а компания не сможет достичь поставленной цели и увеличить прибыль супермаркета. Все дело в том, что исходные предпосылки были ошибочны.
Выводы
Как вы уже поняли, среднее арифметическое зачастую показывает более значимый и приятный результат, как для бизнеса, так и для исследовательских задач, ведь руководству всегда выгоднее представить ситуацию со средним чеком или демографической ситуацией в стране лучше, чем она есть на самом деле. Однако, необходимо всегда помнить о недостатках такой метрики, как среднее арифметическое, чтобы уметь грамотно выбрать подходящий аналог для оценки той или иной ситуации.
Среднее или всё же медиана?
Cреднее арифметическое значение (далее по тексту — среднее), пожалуй, наиболее популярный статистический параметр. Этим понятием пользуются повсеместно — начиная от поговорки «средняя температура по больнице» и кончая серьезными научными трудами. Однако, как ни странно, среднее значение — коварное понятие, часто вводящее в заблуждение, вместо того чтобы придавать четкость изложению и вносить ясность.
Если говорить о научной работе, то статистический анализ данных применяется почти во всех прикладных науках, даже и в гуманитарных (например, психологии). Среднее значение вычисляется для признаков, измеряемых в так называемых непрерывных шкалах. Такими признаками являются, например, концентрации веществ в сыворотке крови, рост, вес, возраст. Среднее арифметическое можно легко вычислить, и этому учат еще в средней школе. Однако (в соответствии с положениями математической статистики) среднее значение является адекватной мерой центральной тенденции в выборке только в случае нормального (гауссова) распределения признака (рис. 1).

В случае же отклонения распределения от нормального закона среднее значение использовать некорректно, так как оно является слишком чувствительным параметром к так называемым «выбросам» — нехарактерным для изучаемой выборки,слишком большим или слишком малым значением (рис. 2). В этом случае для характеристики центральной тенденции в выборке должен применяться другой параметр — медиана. Медиана — это значение признака, справа и слева от которого находится равное число наблюдений (по 50%). Этот параметр (в отличие от среднего значения) устойчив к «выбросам». Заметим также,что медиана может использоваться и в случае нормального распределения — в этом случае медиана совпадает со средним значением.

Для того, чтобы узнать, является ли распределение признака в выборке нормальным (гауссовым) или нет, т.е. для того, чтобы узнать, какой из параметров следует применять (среднее значение или медиану), существуют специальные статистические тесты.
Приведем пример. Скорость оседания эритроцитов в группе пациентов, недавно перенесших пневмонию, — 3, 5, 5, 7, 11, 12, 16, 16, 21, 42, 58. Среднее значение для этой выборки равно 17,8, медиана — 12. Распределение (по тесту Шапиро—Уилка) нормальным не является (рис. 3), поэтому использовать надо медиану.
Как ни странно, но в некоторых областях экономики сторонний наблюдатель не может заметить хоть какого-то следа корректного применения математической статистики. Так, нам постоянно говорят о средней зарплате (например, в НИИ), и эти числа обычно удивляют не только рядовых сотрудников, но и руководителей подразделений (ныне называемых «менеджерами среднего звена»). Мы удивляемся, что средняя зарплата в Москве — 40 тыс. руб., но, конечно, понимаем, что нас «усреднили» с олигархами. Вот пример из жизни научных работников: зарплаты сотрудников лаборатории (тыс. руб.) — 3, 5, 5, 7, 11, 12, 16, 16, 21, 42, 58. Среднее значение — 17,8, медиана — 12. Согласитесь, что это разные числа!
Конечно, нельзя исключить, что замалчивание свойств среднего — лукавство, так как руководству всегда выгоднее представить ситуацию с зарплатой сотрудников лучше, чем она есть на самом деле.
Не пора ли научному сообществу призвать наших руководителей прекратить некорректное использование математической статистики?
Ольга Реброва,
докт. мед. наук, вице-президент
МОО «Общество специалистов доказательной медицины»
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Среднее или медиана что лучше
Сегодня разберем два понятия «среднее» и «медиана».
Для начала задам два вопроса: знакомы ли вы с понятием «медиана»? Знаете ли вы, в чем разница между средним и медианой? Скорее всего, если вы работаете с обзорами по рынку зарплат, вы встречали понятие медианы и чаще всего именно на этом ее применение и заканчивалось. Но я рекомендую использовать медиану и в других случаях.
Среднее – это самый популярный статистический показатель, который используется для измерения центра или середины данных. Среднее значение считается как сумма всех чисел, деленная на общее количество чисел. Это материал где-то пятого класса, поэтому тут пока все просто. Среднее значение в компаниях считают для стажа, возраста сотрудников, зарплаты по грейду, уровню должности, для подачи отчетности по статистическим данным. Считается с помощью функции в Excel: СРЗНАЧ или AVERAGE в английской версии.
Среднее значение может быть не совсем объективным отражением данных, так как на него могут влиять выбросы (очень большие или очень маленькие значения в наборе данных).
Если вы считаете средний стаж работы сотрудников в компании при большой текучести, стаж до трех месяцев работы сотрудников будет занижать данные. Или наоборот, у вас есть сотрудники-старожилы, которые работают с основания компании. При учете их продолжительности стажа вы будете завышать данные, что тоже искажает отчетность.
Пример: рассчитать средний стаж работы сотрудников.
Средний стаж составит 4 года.
Медиана – значение, которое делит отсортированные по возрастанию данных на две равные части. То есть медиана показывает середину ваших данных. Медиана считается как значение, расположенное по середине ряда отсортированных значений. Если в ряду находится нечетное количество данных, например, 5, то медианой будет третье значение. Если четное количество данных, например, 4, то медианой будет (значение 2+ значение 3)/2. То есть среднее значение двух показателей посередине.
Считается с помощью функции в Excel МЕДИАНА или MEDIAN в английской версии. Медиана лишена недостатков среднего значения, на нее не влияют выбросы.
СРЕДНЕЕ vs МЕДИАНА
Не знаю как вы, но я люблю инфографики и статистические данные. С помощью них человек может получить максимальное количество информации за минимальное время. Главное — понимать, что за понятия здесь используются. Например, достаточно часто в статистике используется «среднее значение»: средняя зарплата, средняя продолжительность жизни, средний уровень интеллекта 🙂 и т.д. Сегодня мы посмотрим на сколько обманчивым может быть описание данных с помощью среднего.
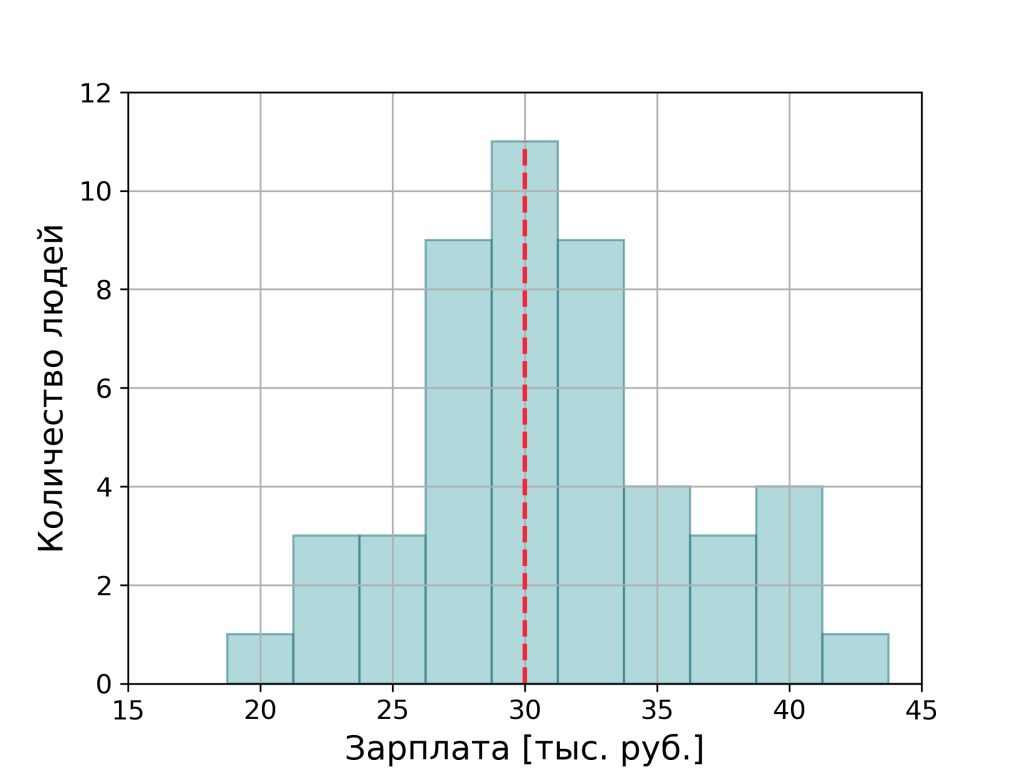
Итак, предположим, сижу я в кинозале. Фильм настолько скучный, что уснуть заняться статистическими расчётами оказалось куда интересней. Решила я подсчитать среднюю зарплату людей в зале. Для этого спросила каждого из 50-ти зрителей, сколько он получает. В результате выяснилось, что 11 человек получают около 30 тыс., 10 человек — 28 тыс., 10 человек — 32 тыс. и т.д. Теперь я могу построить график, отображающий сколько людей получает 20 тыс., 22.5 тыс., 30 тыс. и т.д. :
Кстати, заметьте, величина заработной платы, скорее всего, будет подчиняться распределению Гаусса, о котором мы говорили совсем недавно. Ну а теперь, для того чтобы описать эту группу людей, я подсчитаю среднее значение. Это делается очень просто: складываю зарплаты всех сидящих в зале и делю эту сумму на количество людей. То есть, например, если бы у нас было только 5 человек с зарплатами 30, 30, 25, 28, 15 тысяч рублей, то среднее значение бы равнялось (30+30+25+28+15)/5 = 25.6 тыс. руб. Для группы людей в кинозале я получила среднюю зарплату около 30 тыс. руб. Судя по графику выше, результат выглядит вполне себе логично.
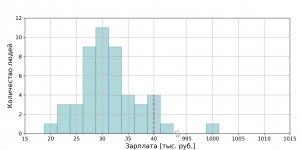
Всё бы ничего, но в середине сеанса в зал заходит продюсер фильма. И вот его зарплата ну уж очень сильно отличается от средней. Предположим, зарабатывает он миллион рублей в месяц. Что же тогда происходит с только что подсчитаной средней зарплатой по кинозалу? Она смещается, при чём смещается очень сильно. Теперь средняя зарплата равна 40 тыс. рублей:
Ну а вот этот результат, мне уже совсем не нравится. Ведь он противоречит тому, что я вижу. По моим ощущениям средняя зарплата по кинозалу не должна быть намного больше 30 тысяч. Но математика говорит иначе. Неужели она лжёт? Нет. Просто в данном случае использовать среднее значение неправильно. Более разумно в этом случае бы было использовать медиану.
Итак, что же это такое? Снова рассмотрим пример с зарплатами пяти человек: 30, 30, 25, 28, 15 тысяч рублей. Чтобы найти медиану нужно эти данные записать в порядке возрастания: 15, 25, 28, 30, 30. Теперь число, находящееся в середине этой последовательности, является медианой (это 28). То есть мне совершенно неважно, равна ли самая большая зарплата этих пятирых 30 тысячам или миллиону. Медиана останется равной 28 тысячам. И она будет более правдоподобно описывать данную группу. Таким же образом я считаю медиану заработной платы людей в кинозале. Даже после прихода продюсера фильма, медиана окажется около 30 тысяч рублей.
То есть описание заработной платы группы людей медианой в нашем случае дало более реальную оценку в сравнении со средним значением. Вот такая вот простая описательная статистика. Так что будьте внимательны к тому, что скрывается за высокопарными статистическими данными и подписывайся на мой телеграм-канал. Вопросы пишите в комментариях. Ну а если статья понравилась, обязательно поделись ссылкой с друзьями в социальных сетях :).
Что лучше использовать при анализе данных: среднее или медиану?
Сегодня разберем два понятия «среднее» и «медиана».
Для начала задам два вопроса: знакомы ли вы с понятием «медиана»? Знаете ли вы, в чем разница между средним и медианой? Скорее всего, если вы работаете с обзорами по рынку зарплат, вы встречали понятие медианы и чаще всего именно на этом ее применение и заканчивалось. Но я рекомендую использовать медиану и в других случаях.
Среднее – это самый популярный статистический показатель, который используется для измерения центра или середины данных. Среднее значение считается как сумма всех чисел, деленная на общее количество чисел. Это материал где-то пятого класса, поэтому тут пока все просто. Среднее значение в компаниях считают для стажа, возраста сотрудников, зарплаты по грейду, уровню должности, для подачи отчетности по статистическим данным. Считается с помощью функции в Excel: СРЗНАЧ или AVERAGE в английской версии.
Минусы среднего показателя:
Среднее значение может быть не совсем объективным отражением данных, так как на него могут влиять выбросы (очень большие или очень маленькие значения в наборе данных).
Если вы считаете средний стаж работы сотрудников в компании при большой текучести, стаж до трех месяцев работы сотрудников будет занижать данные. Или наоборот, у вас есть сотрудники-старожилы, которые работают с основания компании. При учете их продолжительности стажа вы будете завышать данные, что тоже искажает отчетность.
Пример: рассчитать средний стаж работы сотрудников.
Средний стаж составит 4 года.
Медиана – значение, которое делит отсортированные по возрастанию данных на две равные части. То есть медиана показывает середину ваших данных. Медиана считается как значение, расположенное по середине ряда отсортированных значений. Если в ряду находится нечетное количество данных, например, 5, то медианой будет третье значение. Если четное количество данных, например, 4, то медианой будет (значение 2+ значение 3)/2. То есть среднее значение двух показателей посередине.
Считается с помощью функции в Excel МЕДИАНА или MEDIAN в английской версии. Медиана лишена недостатков среднего значения, на нее не влияют выбросы.
Медиана стажа составит 3 года. Разница между 3 и 4 годами стажа работы все-таки есть.
Если нужно посчитать стаж, возраст, зарплату, считайте не среднее, а медиану. Ну или убирайте выбросы.