скремблирование что это такое
Скремблирование цифрового сигнала



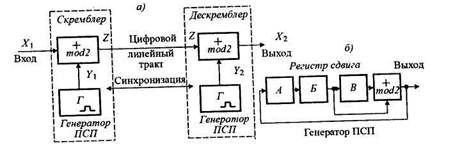
Улучшение ЛЦС с целью упрощения устройств выделения тактовой частоты линейных регенераторов реализуется с помощью процесса, называемого скремблированием, т. е. использования пары преобразующих устройств: скремблера на передаче и дескремблера на приеме (рис. 6.9,а)
Скремблирование заключается в преобразовании исходного двоичного сигнала в сигнал, близкий к случайному, имеющему биноминальное распределение вероятностей появления (при равновероятном появлении символов 1 и 0), т. е. осуществляется рандомизация произвольного информационного сигнала.
В отличие от сигналов спроизвольными статистическими параметрами, для которых вероятности появления символов и групп символов могут быть произвольными, в цифровом случайном (скремблированном) сигнале вероятность появления любой комбинации является не
произвольной, а определяется в соответствии с биномиальным законом вероятностью появления одного символа и длиной серии.
 |
Идея скремблирования основана на том, что, как показано в табл. 6.4, выполненное дважды сложение по модулю 2 передаваемого символа с некоторым другим символом не приводит к его изменению, однако в линию вместо последовательности Х\ передается последовательность Z, имеющая большее число единиц по сравнению с исходной последовательностью.
Основным элементом скремблера является генератор псевдослучайной последовательности (ПСП), схема которого приведена на рис. 6.9,6, а принцип действия иллюстрируется табл. 6.3.
Пусть в начальный момент времени (№ 1) имеет место состояние ячеек памяти А, Б а В регистра сдвига 0, 0 и 1 соответственно, что можно записать как число (001)2 = (1)ю — единицу в двоичной и десятичной системах счисления. Выходной сигнал генератора ПСП равен mod2(E, В) = = mod2(0,.l)=l.
В процессе сдвига в регистре содержимое ячейки В пропадает, содержимое ячейки Б перемещается в ячейку В, содержимое ячейки А перемещается в ячейку Б, а в ячейку А записывается выходной сигнал, т. е. 1.
| № такта | Содержимое ячеек | Число в десятичной системе счисления |
| А | Б | В |
| Линейный тракт цифровых систем передачи по электрическим кабелям | ||
| № такта | Содержимое ячеек | Число в десятичной системе счисления |
| А | Б | В |
Рассмотрим пример передачи цифровой последовательности Хи имеющий вид 10101010 при исходном состоянии генератора ПСП схемы рис. 6.9,6, равном (001)2. Последовательность Z в линейном тракте образуется сложением по модулю 2 последовательности Х\ и выходного сигнала генератора ПСП (содержимое ячейки памяти А в течение тактов № 1. 8). Итак, последовательность Z имеет вид 11110110. Структура последовательности непериодична.
Восстановление дескремблером переданной последовательности на приеме производится по алгоритму Хг = mod2(Z, l^)- Генераторы ПСП на передаче и приеме должны быть синхронизированы. Для этого применяются схемы генераторов с самосинхронизацией, недостатком которых является размножение ошибок, возникающих в цифровом линейном тракте. К достоинствам скремблированного сигнала можно отнести:
— возможность достаточно точного расчета параметров выделителя такто
вой частоты линейных регенераторов, так как может быть определена вероят
ность появления любой комбинации в линейном цифровом сигнале;
— универсальность, которая заключается в возможности сквозной пе
редачи скремблированного сигнала по сети связи через любые циф
ровые тракты, так как скремблирование исходной двоичной последова
тельности осуществляется без преобразования его в другой вид, а выделе
ние исходного сигнала производится только в приемном оборудовании
оконечной станции;
— уменьшение влияния статистических параметров исходного сигна
ла на фазовые дрожания цифрового сигнала в линии;
— обеспечение возможности контроля качества передачи при нарушении чередования полярности импульсов при использовании скремблирования в сочетании с кодом ЧПИ.
Выбор ПСП, наиболее близкой к случайному цифровому сигналу, является достаточно сложной задачей. В качестве наиболее эффективных ПСП предлагается использовать М-последовательности периода N =2″ — 1, образованные полиномами видах 15 + х н + 1 (и = 15) илих 10 + х 9 + х 6 + 1 (п = 10). Далее скремблированный сигнал, как новый ДВС, может быть преобразован в соответствующий код ЛЦС.
На выходе скремблера появляется новая импульсная последовательность, которая систематически связана с исходным ДВС, однако является как бы случайной, поскольку происходит разрушение длинных последовательностей 1 или 0, а также простых периодических последовательностей. Это, естественно, приводит к существенному уменьшению величины систематических фазовых дрожаний.
При установке на магистрали нескольких скремблеров возможно устранение также систематического накопления фазовых дрожаний. Отметим, однако, что если в последовательности, поступающей на вход деск-ремблера, появились ошибки, то при восстановлении сигнала могут возникнуть несколько ошибок.
Размножение ошибок при скремблировании несколько ограничивает область применения данного метода.
6.4. Регенерация цифрового сигнала 6.4.1. Принципы построения и классификации регенераторов
Линейный цифровой сигнал (ЛЦС), проходя по линии связи, испытывает ослабление, подвергается воздействию различного вида помех и искажений, что приводит к деформациям формы и длительности импульсов, уменьшению их амплитуды и случайным временным сдвигам и задержкам сигнала.
Напомним, что с целью снижения межсимвольных искажений форма импульса ЛЦС имеет плавные передний и задний фронты, обеспечивающие минимум последействий переходных процессов, обусловленных ограничениями полосы частот линейного тракта. Для передачи по кабельным линиям используются видеоимпульсы, описываемые, например, функцией вида ДО =
Регенераторы видеоимпульсов, используемые в ЦСП ИКМ-ВРК, можно классифицировать по различным признакам:
— по способу синхронизации по тактовой частоте или получения хро
нирующей информации (далее будем использовать этот термин, как рав
ноправный термину синхронизация по тактовой частоте информации);
— по способу использования хронирующей информации в процессе ре
генерации;
— по виду порогового и решающего устройства.
По способу получения хронирующей информации ЛР можно разделить на регенераторы с самохронированием (или с внутренней синхронизацией) и полным восстановлением временных интервалов и регенераторы с внешним хронированием (или внешней синхронизацией).
В регенераторах с самохронированием колебания тактовой частоты, необходимые для формирования последовательности стробирующих импульсов, выделяются непосредственно из спектра входного ЛЦС. Для выделения хронирующего сигнала используются ранее рассмотренные устройства выделения тактовой частоты (УВТЧ) из спектра ЛЦС. При использовании регенераторов с внешним хронированием к цифровому сигналу примешивается синусоидальный хронирующий сигнал. Этот сигнал может также передаваться по отдельной цепи.
Передача хронирующего сигнала по специальной паре кабеля неэкономична. Кроме того, она сопряжена со значительными трудностями из-за возникающей необходимости точной коррекции фазовых характеристик хронирующей и рабочей пары на каждом РУ с целью получения одинакового группового времени прохождения (ГВП) для частотных составляющих ЛЦС и хронирующего сигнала. Если специальный хронирующий сигнал передается по рабочей паре, то в каждом ЛР необходимо выполнить следующие операции: выделить этот сигнал узкополосными фильтрами; подавить (например, с помощью заграждающих фильтров) составляющие, близкие к тактовой частоте, на выходе ЛР; вновь замешать в линейный сигнал хронирующее колебание. Такие устройства получаются достаточно сложными, но в последнее время в связи с проблемами тактовой сетевой синхронизации находят применение. Поэтому широкое применение получили ЛР с самохронированием с использованием различных способов построения УВТЧ.
Хронирующая информация может быть получена как из входного ЛЦС (регенераторы прямого действия), так и из его выходного сигнала (регенераторы обратного действия). Недостатком регенератора обратного действия является наличие цепи обратной связи, что снижает устойчивость регенератора и повышает требования к стабильности и точности работы его узлов.
По способу использования хронирующего сигнала для управления работой ЛР различают регенераторы с полным и частичным восстановлением временных соотношений (или, как иногда говорят, с полной или частичной регенерацией). В регенераторах с полным восстановлением временных соотношений используется схема выделения тактовой частоты, приведенная на рис. 5.4, на выходе которой формируется стробирующая последовательность импульсов тактовой частоты, управляющая работой ЛР. При частичном восстановлением временных соотношений для выделения тактовой частоты используется только узкополосный фильтр (УФ), напряжение с выхода которого сфазированно таким образом, чтобы положительные (или отрицательные) его полупериоды совпадали с регенерируемыми импульсами, поступающими с выхода порогового устройства ЛР.
Простые алгоритмы скремблирования данных
Иногда нужно что-то зашифровать, но привлекать серьёзные алгоритмы шифрования вроде и не к месту — будет как из пушки по воробьям. Например, нужна простая защита траффика от пользователей/троянов со снифферами, но сами данные не стоят того, чтобы на них тратилось много времени на шифровку-расшифровку, ну и на саму реализацию тоже. Или вам нужно как-то обеспечить закрытость неких хранимых данных от обычных пользователей. Понятно, что подобные алгоритмы не устоят против целенаправленных попыток взлома профессионалами, но мы попытаемся усложнить работу и им, хотя такая задача обычно и не ставится. Вот это-то обычно и называется scrambling.
Под катом я изложу идеи для подобных алгоритмов и обещаю, что они будут посложнее обыкновенного XOR с фиксированым ключом. На всякий случай обращаю внимание на то, что эти алгоритмы не претендуют на звание криптостойких, но уверен, что вы сможете найти им применение.
Предпосылки
Предполагается, что потенциальный взломщик либо не имеет доступа к коду, который осуществляет шифрование, либо не имеет достаточной квалификации для реверс-инжениринга, либо данные не настолько ценны, чтобы тратить время на более тяжёлые методы взлома.
Наверно все знают, что в подобных случаях чаще всего применяют простое циклическое наложение ключа фиксированой длины с помощью операции XOR. И все так же хорошо знают, что такая защита не выдерживает даже начинающего «хакера» или продвинутого пользователя. Хотелось бы что-нибудь посложнее, но простое в реализации.
А если генерировать ключ?
Первое, что приходит в голову, это генерировать достаточно длинный ключ, чтобы хотя бы усложнить нахождение длины ключа. Например, использовать некий генератор псевдослучайных чисел с входными данными, известными и отправителю, и получателю. Один из таких часто применяемых генераторов — линейный конгруэнтный ГПСЧ (ГСПЧ это генератор псевдослучайных чисел). Мы, конечно, догадываемся, что это плохо, но что же именно плохо в этом подходе? Проблема в том, что довольно трудно генерировать параметры для самого генератора. Программно подобрать хорошие параметры для линейного конгруэнтного ГПСЧ, чтобы последовательность была длинная и невырожденая, довольно трудно. По этому поводу можно почитать в 3.2.1 в книге Д.Кнута «Искусство программирования». Поэтому зачастую эти параметры вколачивают в код как константы и, как следствие, потенциальный взломщик получает множество сообщений зашифрованых с одним ключом, что значительно упрощает его работу.
А что если использовать сами данные для генерации этой псевдослучайной последовательности?
Эта идея осенила меня лет 20 назад, когда я «помогал» писать диплом одной моей знакомой студентке. На первый взгляд кажется, что это невозможно, ведь нам нужен генератор, который выдавал бы одинаковую последовательность и при шифровке, и при расшифровке. Как ни странно, именно этот «убийственный» тезис и даёт нам путь к созданию такого генератора. Да, нам нужен алгоритм, который меняет значения своих внутренних переменных одинаково, если ему дать исходный байт (или что там у нас является атомарной единицей кодирования) и зашифрованый байт. Как этого достичь? Всё гениальное просто — для вычисления следующего значения ключа можно задействовать коммутативные операции для пар исходных-шифрованых байт. Так как результат операции не зависит от порядка операндов в паре, то очевидно, что такой алгоритм будет менять свои переменные при расшифровке точно так же как и при шифровке, но последовательность ключей для других входных данных будет другой.
Пример генератора ключей, зависящего от входных данных
Чтоб было понятней, рассмотрим простенький пример такого алгоритма.
Пусть xn — это очередной код в исходных данных, kn — текущий ключ, kn+1 — следующее значение ключа, yn — зашифрованый код xn.
Q(a,b) — некая коммутативная функция, т.е. такая, что q(a,b)==q(b,a).
F(a,b,c) — некая целочисленная функция.
Toгда итерацию по (де)кодированию можно описать так:
yn := xn xor kn;
kn+1 := F( kn, Q( xn, yn ), n );
Если для функции F() понятно, что её имплементация в общем-то ограничена лишь нашей фантазией и здравым смыслом, то про Q(), вероятно, вам хочется увидеть подробностей, а именно, каким таким условиям она должна соответствовать, чтобы быть коммутативной. Самый простой способ этого достичь — использовать аргументы только парами в коммутативных операциях, например xor, сложение, умножение. Примеры: Q(a,b) = a xor b. (Исправлено: пожалуй я тут погорячился, ведь при наложении исходного и зашифрованного кода получается ключ, что нежелательно. Я лично использую немного более сложные функции).
Q(a,b) = ((a xor b) or 1) * (( a + b ) xor 1).
Как видите, придумать свою супер-пупер функцию Q() совсем не сложно. Другое дело, нужно ли её делать сложной? Думаю, что особого смысла в её переусложнении нет.
Ну а теперь-то что плохо?
А ещё идеи есть?
А то! У меня всегда есть идеи!
Допустим вы передаёте данные в сжатом виде. Или данные уже частично зашифрованы. Или каждое сообщение/блок достаточно длинные и состоят из двоичных данных с примерно равномерным распределением кодов. В этом случае любое вмешательство в порядок кодов в сообщении может существенно усложнить жизнь потенциальному взломщику. Уверен, что вы можете и сами придумать некий примитивный перемешиватель байтов в блоке данных, но я ведь обещал интересные и красивые идеи.
Перемешиватель данных (shuffler)
Обычно для решения этой задачи используют некий ГСПЧ для получения пар индексов кодов в блоке данных, которые меняют местами. Неприятность этого метода в том, что трудно гарантировать, что какая-то часть данных не останется на том же месте. Также не совсем понятно, сколько же перестановок нужно сделать, чтобы достичь приемлемого результата, хотя для надёжности можно просто пройтись по всем кодам сообщения и обменять каждый со случайным. Но есть ещё одна неприятность — если генератор имеет плохое распределение по квадрату (а линейный конгруэнтный именно такой болезнью и болеет, и причём безнадёжно), то при определённых размерах блока можно нарваться на зацикливание выдаваемых значений. Я довольно долго шёл к идее быстрого псевдослучайного перемешивателя данных (shuffler) и считаю, что она заслуживает вашего внимания не только как алгоритм для скремблирования.
Немного теории. В пункте 3.2.1.2 книги Д.Кнута «Искусство программирования» можно найти критерии для выбора множителя для линейного конгруэнтного генератора, чтобы длина генерируемой последовательности равнялась модулю. Что это означает? Это значит, что для генератора с модулем m каждое значение от 0 до m-1 будет выдано ровно один раз. Зачем это нам? Вспомним, что для нашего перетасовщика было бы желательно гарантировать, что все байты(коды) сообщения поменяли своё место. То есть, если длина данного блока данных равна этому самому m, то нам будет достаточно просто записывать очередной входной байт(код) сообщения в выходной буффер по индексу, равному очередному значению из генератора. Простота этого алгоритма настолько сооблазнительна, что я не мог пройти мимо.
Но, как всегда случается с чем-то сооблазнительным, не обошлось без проблем. Во-первых, не все m одинаково полезны хороши. Из той же главы той же книги мы видим, что если m является произведением простых чисел в первой степени, то полного перебора элементов мы достичь не можем в принципе (не считая перебора подряд, что нам, конечно, не интересно). Получается, что получить нужный нам генератор с заданной длиной последовательности нельзя, и, следовательно, если у нас сообщения произвольной длины, то мы не всегда можем найти такой генератор. Тупик? А действительно ли нам нужны генераторы произвольной длины? Вспомним о том, что для потенциального взломщика знание длины сообщения очень даже небесполезно. Тогда мы уже знаем и способ борьбы, который мы успешно применяли для генератора, зависящего от входных данных. Правильно, надо подбросить случайный мусор, и лучше всего перед полезными данными. Правда, есть проблема в том, что в каждом блоке нужно как-то указывать количество полезной информации в нём. Если же в вашем случае длина всех сообщений/блоков данных фиксирована, то вы вы можете зафиксировать и m — выбрать первое удобное для вас значение, которое больше длины входного блока и удовлетворяет критерию из теоремы A из 3.2.1.3 из книги.
Ещё идеи?
Довольно очевидна идея объединить shuffler и генератор, зависящий от данных. Для этого мы сначала скармиваем генератору нужное количество мусора, чтобы подогнать длину сообщения под размер блока shuffler’а, а потом уже прогоняем данные самого сообщения. Все выходные коды пишем по индексам, которые получаем от shuffler.
Думаю, что на сегодня хватит.
Исправления: Исправил замеченную отчепятку и зачеркнул неудачный пример.
Скремблер: надёжно и просто
Эта статья написана для того, чтобы рассказать читателю, что такое скремблеры, обозначить области их применения и затронуть некоторые практические тонкости, а также раскрыть секреты алгоритма скремблирования.
Зачем и почему?
Иногда возникает необходимость зашифровать трафик, не прибегая к методам, требующим много времени и ресурсов на шифровку и расшифровку, а также реализацию алгоритма. Такое случается, когда мы стараемся защитить данные от пользователей или примитивных троянов со снифферами (анализаторами трафика), но эти данные не стоят того, чтобы прибегать к серьезным методам шифрования, так как нам не требуется высокая криптостойкость. Со стороны методов связи бывает необходимо уменьшить уровень излучаемых помех, распределив энергию равномерно, и повысить надежность синхронизации устройств. С этими задачами и справляется скремблирование.
Что же такое скремблер?
Скремблер (от англ. to scramble – перемешивать, шифровать) – это алгоритм, разработанный для побитной последовательной передачи информации, позволяющий зашифровать цифровой поток таким образом, что на выходе получается последовательность, обладающая свойствами случайной: равновероятным появлением нуля и единицы. Именно это позволяет надежно выделить тактовую частоту и постоянную мощность передаваемого сигнала, что и дает надежность синхронизации. Стоит отметить, что такое преобразование потока не меняет скорость передачи, а также является обратимым, то есть данные восстанавливаются обратным алгоритмом.
Как это работает?
У нас имеется передающая сторона, на которой выполняется скремблирование, а также принимающая сторона, на которой соответственно выполняется дескремблирование, то есть обратная операция. Исходная последовательность подается на вход скремблера, а также именно она выделяется дескремблером из принятой зашифрованной последовательности.
Главной частью скремблера является линейный n-каскадный регистр сдвига с обратными связями, генерирующий псевдослучайную последовательность (ПСП) максимальной длины . Основная операция, производимая при шифровании – сложение по модулю 2, то есть XOR (исключающее ИЛИ).
Типы скремблеров
По типу взаимодействия с регистром скремблеры делятся на два типа: самосинхронизирующиеся (СС-скремблеры) и аддитивные (АД-скремблеры или же скремблеры с установкой). И те, и другие имеют свои плюсы и минусы, которые станут ясны после более подробного рассмотрения алгоритмов.
СС-скремблер
Отличительной чертой самосинхронизирующегося скремблера является то, что шифрование производится на основе самой скремблированной последовательности, поступающей на вход регистра сдвига. Следствием этого является отсутствие необходимости предустановки состояний скремблера и дескремблера в идентичное начальное состояние, синхронизация происходит сама по себе. При потере синхронизации восстановление состояния не превышает числа тактов, равного числу ячеек регистра скремблера.
Сам алгоритм скремблирования в этом случае можно рассмотреть на простейшем примере.

Несложно заметить, что при выполнении такого алгоритма большую опасность представляет «лавинный эффект» вследствие размножения ошибок. Это происходит именно из-за того, что для шифрования каждого следующего бита используется результат шифрования предыдущих. А значит, что при ошибке в одном бите мы получим уже n неправильно зашифрованных бита (где n – число обратных связей регистра), которые впоследствии приведут к ошибке в 2n и так далее. Другой проблемой самосинхронизирующихся скремблеров является то, что первые k битов входящей последовательности в принципе не будут зашифрованы. К счастью, этого легко избежать искусственным добавлением шума в начало последовательности.
АД-скремблер
Аддитивные скремблеры не получают на вход регистра результат шифрования, чем избегают распространения ошибок и лавинного эффекта, однако скремблер и дескремблер требуют предварительной установки состояния регистра – ключа. На вход регистра поступает линейная комбинация уже находящихся в нем бит, она же суммируется с входящим сигналом, в результате чего и получается зашифрованная последовательность.
Сам алгоритм скремблирования в этом случае можно рассмотреть на простейшем примере.

На практике чаще всего применяются именно аддитивные скремблеры, так что далее проанализируем особенности этого алгоритма.
Синхронизация
В АД-методе скремблирования важную роль играет синхронизация состояний регистров скремблера и дескремблера, ведь при ее потере вся дальнейшая информация неизбежно теряется. Для поддержания синхронизации на практике используются такие методы, как добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении такого бита активно начать поиск синхронизации с отправителем, и использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить декодирование принимаемых битов информации «по памяти» без синхронизации. Стоит отметить, что именно необходимость в синхронизации скремблеров привела Джеймса Х. Эллиса к идее криптосистем с открытым ключом, что впоследствии привело к созданию алгоритма шифрования RSA и протокола Диффи-Хеллмана.
Зацикливание и построение алгоритма
Разрядность скремблера – разрядность устройства памяти – идентична длине ключа для блочных шифров. От нее напрямую зависит криптостойкость данной системы. При длительном скремблировании неизбежно возникает зацикливание, то есть через определенное число тактов регистр возвращается в исходное состояние, после чего шифрование будет циклически повторяться. Это повторение происходит непосредственно из-за того, что в n ячейках регистра возможны только комбинаций бит, а значит, максимум через
комбинаций состояние станет идентичным начальному. А значит, мы хотим достигнуть именно этой максимальной длины.
К счастью, для скремблера любой разрядности n существует такая комбинация обратных связей, при которой период реализуем. То есть за
тактов значения в регистре ни разу не повторятся. Оказывается, для этого достаточно, чтобы скремблер был построен на основе неприводимого полинома степени n, не представимого по модулю 2 в виде произведения никаких других полиномов. Выбранные таким способом обратные связи и используются в схемах скремблирования, при этом мы получаем генератор последовательностей наибольшей длины (ПНД).
Алгоритм построения следующий:
находим неприводимый полином степени n
отбрасываем старший разряд в его двоичном представлении, так как он несет информацию только о степени этого полинома
по полученному двоичному представлению строим скремблер, 1 на соответствующих разрядах говорят о наличии обратной связи, 0 – об ее отсутствии
Так, например, для 15-ти разрядного регистра мы имеем неприводимый полином с двоичным представлением 1000000000000011 . После отбрасывания старшего бита получаем 000000000000011 , то есть скремблер с алгоритмом:
.
Что в итоге?
Скремблирование – достаточно простой алгоритм, используемый для шифрования алфавитно-цифровой, графической, а также речевой информации для последующей передачи ее по системам связи.
Современные скремблеры несколько отличаются от их более ранних аналогов, так как для повышения криптостойкости совмещаются с асимметричными алгоритмами шифрования.
Тем не менее скремблеры повсеместно применяются и сейчас, как из-за простоты реализации, так и из-за других очевидных преимуществ данного алгоритма.



