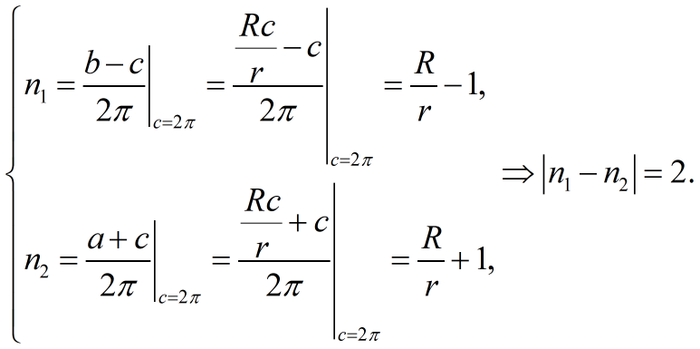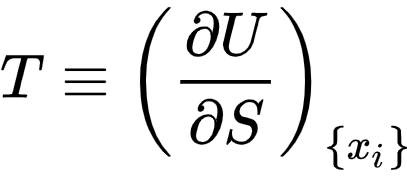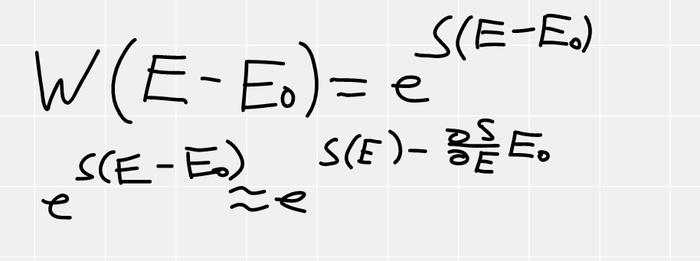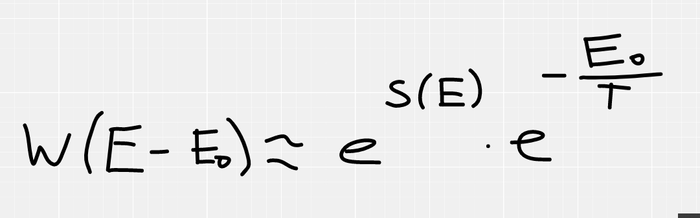интерстеллар гаргантюа что это
Что такое Гаргантюа?
Гаргантюа — очень массивная, быстро вращающаяся черная дыра. Она вращается вокруг планет Миллер и Манн, а также безымянной нейтронной звезды.
Звезда главной последовательности Пантагрюэль находилась в пределах годового полета от Гаргантюа вместе с обитаемой планетой Эдмундс. Гаргантюа находится в пределах нескольких недель космического полета к Червоточине.
В книге Кипа Торна «The Science of Interstellar» он упоминает, что Гаргантюа не имеет струи или перегретого синего аккреционного диска, что указывает на то, что она, вероятно, не пожирала звезду миллионы лет.
История
Одним из первых открытий НАСА после отправки первых зондов через Червоточину, вероятно, была Гаргантюа. Миссии Лазаря очень мало занимались изучением Гаргантюа, но межзвездный зонд НАСА определил ее гравитационное влияние на планетную систему.
Черная дыра Гаргантюа использовалась для гравитационного маневра, чтобы облегчить прибытие Брэнда на планету Эдмундса, поскольку у Endurance не было достаточно топлива, чтобы добраться до Эдмундса самостоятельно.
Гаргантюа также доставил Купера и ТАРС к тессеракту, что позволило им увидеть сингулярность черной дыры и передать квантовые данные дочери Купера с помощью кода Морзе. Предположительно, Гаргантюа находится в центре галактики или недалеко от него. Из-за наличия большого количества нейтронных звезд и IMBH (черных дыр промежуточной массы) это могла быть сверхмассивная черная дыра домашней галактики.
Сценарий 2008 года
Названия нейтронной звезды и черной дыры, скорее всего, взяты из «Жизни Гаргантюа и Пантагрюэля», пентологии романов, написанных в XVI веке Франсуа Рабле и повествующих о приключениях двух гигантов: Гаргантюа и его сына Пантагрюэля.
В сценарии 2008 года Пантагрюэль на самом деле представляет собой меньшую черную дыру с ледяной планетой, вращающейся вокруг нее.
Дополнительные подробности из «The Science of Interstellar»
По расчетам Кипа Торна, масса Гаргантюа составляет около 100 миллионов солнечных масс, что делает ее сверхмассивной черной дырой.
Некоторые визуальные эффекты были сильно приглушены по сравнению с тем, как это могло бы выглядеть на самом деле; горизонт событий будет искажен, а красный и синий будут смещены.
Планета Миллер находилась бы ниже уровня аккреционного диска, а горизонт событий покрыл бы 40% видимого неба. Согласно тем же расчетам, орбитальные переходы к Миллеру, вероятно, потребуют гравитационных маневров вокруг черных дыр промежуточной массы как в начале маневров, так и в конце, поскольку потребности в топливе, по-видимому, исключают другие методы получения необходимой энергии.
FAQ ПО ГАРГАНТЮА: РЕАЛЬНА ЛИ ЧЕРНАЯ ДЫРА В ИНТЕРСТЕЛЛАР? Часть 2
А ссылку на первоисточник почему не дали? Статья ведь не ваша.
Вдогонку к посту «Прыгаем в чёрную дыру»
Бонусное видео с прыжком в чёрную дыру. Без комментариев и под атмосферное музыкальное сопровождение. Сделано в формате 360 градусов, так что можно покрутить и наблюдать от первого лица эффекты, описанные в основном видео с теорией.
Мнимые числа для описания реальности?
Новый мысленный эксперимент показывает, что квантовая механика не работает без странных чисел, которые становятся отрицательными при возведении в квадрат.
Много веков назад математики были обеспокоены, когда обнаружили, что вычисление свойств определенных кривых требует, казалось бы, невозможного: чисел, которые при умножении сами на себя становятся отрицательными.
Все числа на числовой прямой, возведенные в квадрат, дают положительное число; 22 = 4 и (-2)2 = 4. Математики начали называть эти знакомые числа «вещественными», а, казалось бы, невозможную разновидность чисел — «мнимыми».
Однако физики, возможно, только что впервые показали, что мнимые числа в определенном смысле вещественны.
Группа теоретиков в области квантовой физики разработала эксперимент, результат которого зависит от того, есть ли у природы мнимая сторона. При условии, что квантовая механика верна — предположение, с которым мало кто поспорит, — аргумент команды по существу гарантирует, что комплексные числа являются неизбежной частью описания материальной вселенной.
«Эти комплексные числа обычно являются просто удобным инструментом, но здесь оказывается, что они действительно имеют какое-то материальное значение», — сказал Тамаш Вертези, физик из Института ядерных исследований Венгерской академии наук, который много лет назад утверждал обратное. «Мир таков, что ему действительно нужны эти комплексные числа», — сказал он.
В квантовой механике поведение частицы или группы частиц выражается волнообразным объектом, известным как волновая функция или ψ. Волновая функция прогнозирует вероятные результаты измерений, такие как вероятное положение или импульс электрона. Так называемое уравнение Шрёдингера описывает, как волновая функция изменяется во времени — и это уравнение включает i.
Физики никогда не знали, что с этим делать. Когда Эрвин Шрёдингер вывел уравнение, которое теперь носит его имя, он надеялся избавиться от i. «Что неприятно и против чего прямо следует возражать, так это против использования комплексных чисел, — писал он Хендрику Лоренцу в 1926 году, — Ψ, безусловно, является вещественной функцией».
Желание Шрёдингера, безусловно, было правдоподобным с математической точки зрения: любое свойство комплексных чисел может быть зафиксировано комбинациями вещественных чисел, а также новыми правилами, открывая математические возможности полностью вещественной версии квантовой механики.
Действительно, переход оказался достаточно простым, так что Шрёдингер почти сразу открыл то, что он считал «истинным волновым уравнением», которое «сторонилось» i. «Еще один камень с души упал», — написал он Максу Планку менее чем через неделю после своего письма Лоренцу. Все вышло именно так, как хотелось.
Но использование вещественных чисел для моделирования сложной квантовой механики неудобное и абстрактное занятие, и Шрёдингер признал, что его полностью вещественное уравнение слишком громоздко для повседневного использования. В течение года он описывал волновые функции как комплексные, в том виде, в каком их представляют сегодня физики.
«Любой, кто хочет выполнить работу, использует комплексное описание», — сказал Мэтью МакКейг, учёный в области информатики из Технологического университета Квинсленда в Австралии.
Однако формулировка квантовой механики с помощью вещественных чисел сохранилась как свидетельство того, что комплексная версия просто необязательна. Например, команды, включая Вертези и МакКейга, показали в 2008 и 2009 годах, что и без i они могут идеально предсказать результат известного эксперимента в квантовой физике, известного как тест Белла.
Новое исследование, которое было опубликовано на сервере научных препринтов arxiv.org в январе, обнаружило, что ранние предложения по тестам Белла просто недостаточно продвинулись, чтобы опровергнуть версию квантовой физики с вещественными числами. Это исследование предлагает более сложный эксперимент Белла, который, похоже, требует комплексных чисел.
Ранние исследования привели людей к выводу, что «в квантовой теории комплексные числа лишь удобны, но не необходимы», — писали авторы, в число которых входят Марк-Оливье Рену из Института фотонных наук в Испании и Николя Жизен из Женевского университета. «Мы доказываем ошибочность этого вывода».
Группа отказалась публично обсуждать свою работу, поскольку он все еще находится на экспертной оценке.
Тест Белла показывает, что пары удаленных друг от друга частиц могут обмениваться информацией в едином «запутанном» состоянии. Если бы монета 25 центов в штате Мэн могла «запутаться», например, с такой же монетой в Орегоне, то повторяющиеся подбрасывания показали бы, что всякий раз, когда одна монета падает орлом, ее дальний партнер, как ни странно, выпадет решкой. Точно так же в стандартном эксперименте теста Белла запутанные частицы отправляются двум физикам с вымышленными именами Алиса и Боб. Они измеряют частицы и, сравнивая измерения, обнаруживают, что результаты коррелированы таким образом, что это не поддаётся объяснению, разве что частицы обмениваются информацией.
Модернизированный эксперимент добавляет второй источник пар частиц. Одна пара достается Алисе и Бобу. Вторая пара, «родом» из другого места, отправляется Бобу и третьему лицу, Чарли. В квантовой механике с комплексными числами частицы, которые получают Алиса и Чарли, не обязательно должны быть запутаны друг с другом.
Однако никакое описание в виде вещественных чисел не может воспроизвести модель корреляций, которую будут измерять три физика. В новой статье показано, что рассмотрение системы как вещественной требует введения дополнительной информации, которая обычно находится в мнимой части волновой функции. Частицы Алисы, Боба и Чарли должны разделять эту информацию, чтобы воспроизводить те же корреляции, что и в стандартной квантовой механике. И единственный путь приспособиться к этому разделению — это перепутать все их частицы друг с другом.
В предыдущих воплощениях теста Белла электроны Алисы и Боба поступали из одного источника, поэтому дополнительная информация, которую они должны были нести в описании вещественных чисел, не представляла проблемы. Но в тесте Белла с двумя источниками, где частицы Алисы и Чарли происходят из независимых источников, фиктивная трехсторонняя запутанность не имеет физического смысла.
Даже без привлечения Алисы, Боба и Чарли для фактического проведения эксперимента, который представляет новая статья, большинство исследователей крайне уверены, что стандартная квантовая механика верна и, следовательно, эксперимент найдет ожидаемые корреляции. Если это так, то одни только вещественные числа не могут полностью описать природу.
«В статье устанавливается, что существуют истинные комплексные квантовые системы», — сказал Вальтер Моретти, физик-математик из Университета Тренто в Италии. Этот результат стал для него совершенно неожиданным.
Тем не менее велика вероятность того, что когда-нибудь эксперимент состоится. Это будет непросто, но технических препятствий нет. И глубокое понимание поведения усложняющихся квантовых сетей будет становиться все более актуальным, поскольку исследователи продолжают связывать многочисленные Алисы, Бобы и Чарли через возникающие квантовые сети.
«Поэтому мы верим, что опровержение вещественной квантовой физики произойдет в ближайшем будущем», — пишут авторы.
Автор оригинала: Charlie Wood
Прыгаем в чёрную дыру (ScienceCLic)
Как выглядит чёрная дыра? Какие оптические эффекты возникают в непосредственной близости от неё? Что мы увидим при пересечении горизонта событий?
Для визуализации использовались расчёты и симуляции.
Реставрирую шкаф
Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.
Ответ на пост «Вопрос к лиге физиков»
Итак, задача любопытная и потому приступим.
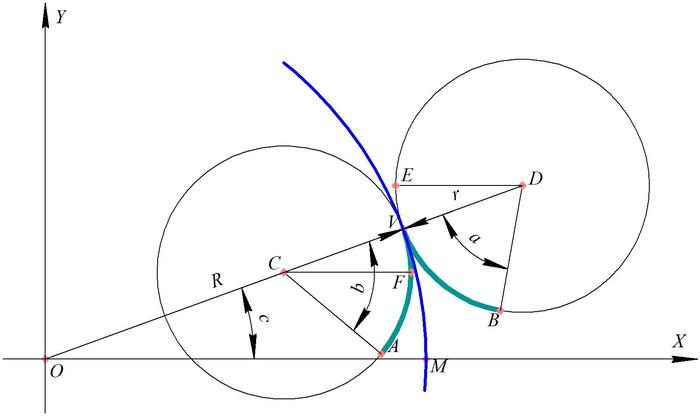
Ставится задача по определению отношения или разности сделанных оборотов двух окружностей равного радиуса r по окружности радиуса R (снаружи и внутри). Составим расчётную схему.
Сразу становится понятно как определить количество оборотов окружностей. А именно:
Выразим теперь углы a и b как некие функции от угла с. Для это отметим, что поскольку в условии отсутствует скольжение, то
Используем равенство соответственных и накрест лежащих углов и тогда для искомых углов имеем:
Объединим всё вместе:
Итого, разность составляет два оборота.
P. S. Любопытно, к слову, что отношение длин траекторий выражается отношением разности радиусов неподвижной и подвижной окружностей к их сумме.
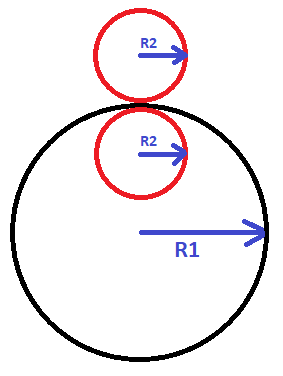
Вопрос к лиге физиков
В 7 классе участвовал в городской олимпиаде по физике. Не решил я, по-моему, ни одной задачи, а попал туда потому что от нашей школы больше посылать было просто некого. Одну из задач помню до сих пор, и до сих пор не понимаю как ее решать, даже имея диплом, в котором написано «математик».
Вопрос: когда обе окружности радиусами R2 придут в ту же точку, с которой начали, каково будет отношение количества оборотов, сделанное внешней и внутренней окружностями?
Температура, что это?
В своём прошлом посте я остановился на том, что о температуре как физической величине, люди мало что знают. В школе так вообще отделываются лишь «мерой движения молекул» и на этом заканчивают. А ведь это довольно любопытная штука, смысл которой далеко за простой «средней энергией частиц». Давайте попробуем разобраться, что про неё известно и какие определения температуры есть, и можно ли как-то например дать температуру одной молекуле.
Если копаться всерьез, то очень больно для головы. Потому что количество определений для температуры слишком большое. У разных разделов физики порой разные определения, так и даже в самой термодинамике есть куча вариантов аксиоматики. На одной вики их штук 10, если копать научные статьи, то вполне можно еще десяток другой вариантов найти. Мы не полезем в эти дебри и разберем лишь два определения, первое из классической термодинамики, второе из статистической физики (в которой становится понятнее, как всё же её пощупать можно).
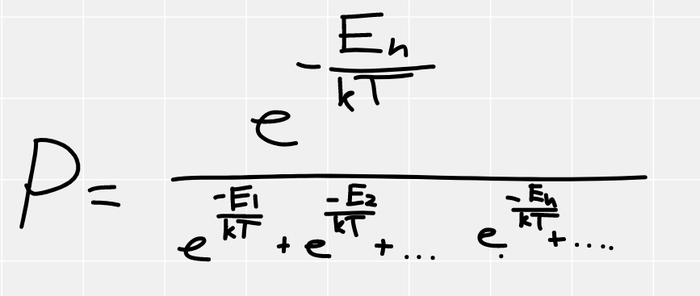
Если грубо разделить аксиомы классической термодинамики на две группы, то в одних аксиоматических построениях температуру просто постулируют как некую физическую величину, которая просто есть (неопределяемая переменная), является интенсивной величиной и количественно выражает интуитивное понятие о различной степени нагретости тел. В других построениях, как неопределяемую базовую переменную вводят энтропию, а температуру определяют как частную производную энергии от энтропии.
Хоть эта запись и пугает всех, кто не знаком с курсом математического анализа, на человеческом языке, она означает «температура это скорость роста энергии при росте энтропии, при неизменном объеме, массе веществ, площади поверхностей и т.д.»
Отлично, а что там в статистической физике? Ну условно, там та же формула, что и на картинке выше. Но лучше показать на простейшем примере.
Для примера я возьму систему с десятью монетками. Давайте договоримся, что если монетка орлом вверх, то она имеет энергию 0, если решкой вверх, то энергия такой монетки будет у нас 1.
У системы на картинке энергия 2. У системы с десятью орлами, энергия будет 0. В прошлом посте я объяснял, как считают энтропию в статистике. Так что давайте посчитаем сколько микросостояний дает нам разную энергию.
E = 0 можно получить имея все монетки орлом вверх, это одно состояние, энтропия 0.
E = 1 можно получить имея одну решку, она может быть на первом, втором. и т.д. месте, микросостояний 10, энтропия k*ln10
E = 2 еще больше вариантов, их 45, а энтропия k*ln45
E = 3, вариантов 120, энтропия k*ln120
Реальные физические системы с таким простым набором состояний существуют, например система спинов в магнитном поле: типичная начинка квантового компьютера, атомы водорода в ЯМР спектрометре или они же в томографе.
У обычных больших тел (стакан воды, суп на плите, пробирка) квантовых состояний в невероятное количество раз больше, но с ростом энергии количество возможных вариантов аналогично растет, функцию E(S) можно вполне себе считать непрерывной. Для макрообъектов расстояние между уровнями энергии настолько мало, они так сгущаются, что измерить этот зазор невозможно даже в теории. Энтропию можно ввести и через классическую механику, рассматривая молекулы как шарики, правда там немного иначе она будет считаться, но ответ совпадает с квантовым рассмотрением.
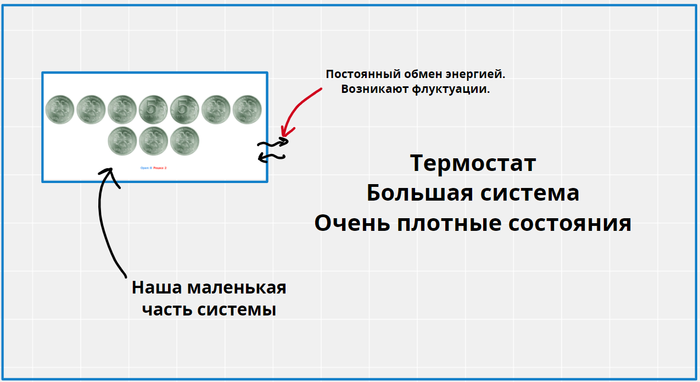
Внимательные наверное уже заметили, что в определении температуры формула содержит производную, а в примере у меня дискретная функция, у которой нельзя посчитать производную. Именно так, понятие температуры в строгом смысле работает только для макроскопических объектов с кучей уровней, где мы не можем заметить, что функция E(S) дискретная. Для описания температуры объектов с малым количеством уровней, приходится сначала утверждать, что такая система находится в состоянии термического равновесия с термостатом (модельная среда, с конкретной температурой), но тогда наша система уже не имеет конкретную энергию, и имеет лишь вероятности находиться на том или ином уровне, ведь между маленькой системой и большим термостатом возникают флуктуации. Эти вероятности легко посчитать, пользуясь нашими формулами. Собственно для маленьких систем, температура уже будет иметь немного другой смысл, и быть скорее параметром, который описывает распределение вероятностей по уровням. О как!
Возьмем всё ту же систему с монетками, и попробуем выяснить как температура окружающей среды будет влиять на её энергию. Представим, что она находится в равновесии и контакте с какой-то другой системой, огромной по сравнению с ней, но при этом конечной.
Всё вместе мы представим изолированной системой с энергией E. Попробуем найти вероятность быть нашей системе в каком-нибудь состоянии с энергией E0.
У нас вся система, обладает каким-то набором микросостояний, пусть их W штук. Нам просто нужно найти сколько из них, подходят нам и поделить это число на общее количество.
Если наша подсистема, в состоянии с энергией E0, то на термостат остается E-E0. Учитывая, что W=exp(S), получаем, что вероятность пропорциональна exp(S(E-E0)), но как это посчитать? Мы не зря посчитали, что термостат НАМНОГО больше чем наша подсистема, поэтому E0
Во всем выводе я убрал константу Больцмана, считайте, что я принял её единичкой, это не так важно.
В формуле появилась производная энтропии от энергии (что есть 1/T по определению из начала поста). И в конце концов мы получаем
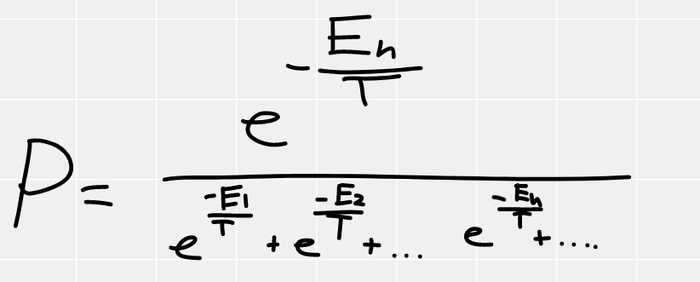
Вероятность должна быть пропорциональна W, при этом в сумме они все должны давать единичку, поэтому вероятность нашей маленькой системке находиться в n-ом состоянии (у которого энергия En), будет
Если вернуть везде постоянную Больцмана, получится так
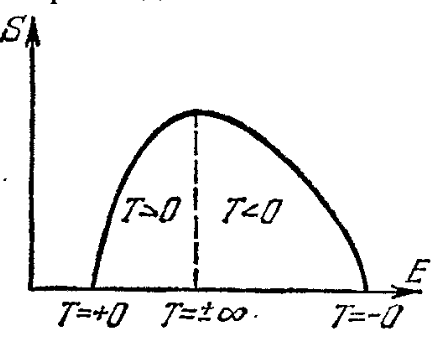
Снизу в формулах энергии всех остальных уровней. Очень симпатичная формула, называется распределением Гиббса. Из неё можно вывести распределения Максвелла, Больцмана и прочие прекрасные частные случаи. По ней видно, что если температура абсолютный ноль, то система находится в низшем состоянии с вероятностью 1, если же температура бесконечна, то система равновероятно может находиться во всех состояниях от низшего до наивысшего, что немного контринтуитивно (кажется, что бесконечная температура, это наивысшее состояние по энергии), но как видите это не так. Температура это сложный статистический параметр, а не просто энергия тела как нам кажется интуитивно.
Еще один интересный вывод из такой формулы вытекает если наша система имеет конечное количество состояний (как наш пример с монетками имеет всего 1024 состояний, и 10 уровней), то возможно представить себе отрицательную температуру. Это состояние будет отвечать энергии системы даже большей чем, энергия системы при бесконечной температуре, ибо высшие уровни заселены чаще чем низшие (при бесконечной они поровну все заселены). Мы можем создать искусственно такие состояния в реальности, ведь системы с ограниченным количеством уровней существуют, а способы «перевернуть заселенность» существуют.
Но откуда же у нас всех берется знание, что температура отвечает за скорость молекул? А дело в том, что если мы применим распределение Гиббса к идеальному газу, то средняя кинетическая энергия молекулы будет 3/2kT, об этом нам рассказывают в школе сразу в готовом виде (исторически температуру с этого случая вводили и в науке), и на этом же эту тему заканчивают, отсюда и остается подобный обрубок понимания довольно сложного понятия температуры.
Учитывая, что статистическая физика и термодинамика стоят на очень простых принципах из математики, выходит довольно любопытная ситуация. Дело в том, что и общая теория относительности, и квантовая механика отлично стыкуются с термодинамикой. Но как мы знаем, между собой ОТО и КМ очень плохо стыкуются, и квантовую теорию гравитации до сих пор не разработали. Так же мы знаем, что внутренности и поверхности черных дыр, обладая страшной кривизной пространства-времени, должны описываться той самой пока несуществующей квантовой теорией гравитации, но мы точно понимаем, что эта теория должна тоже хорошо стыковаться с термодинамикой. Изучение термодинамики черных дыр сразу показало, что они должны обладать температурой и излучать, позже Хокинг более подробно описал это излучение, которое назвали в его честь, но это уже совсем другая история.
Закончу пост цитатой Эйнштейна:
«Теория производит тем большее впечатление, чем проще ее предпосылки, чем разнообразнее предметы, которые она связывает, и чем шире область ее применения. Отсюда глубокое впечатление, которое произвела на меня классическая термодинамика. Это единственная теория общего содержания, относительно которой я убежден, что в рамках применимости ее основных понятий она никогда не будет опровергнута»
Эйнштейн А. Собр. науч. трудов М.: Наука, 1967. Т. 4. с. 270
Что, если наш 4D мир станет пятимерным?
Краткая текстовая версия видео:
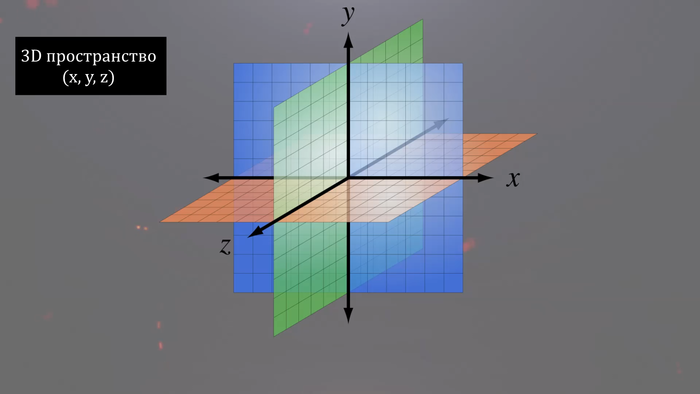
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».
В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?
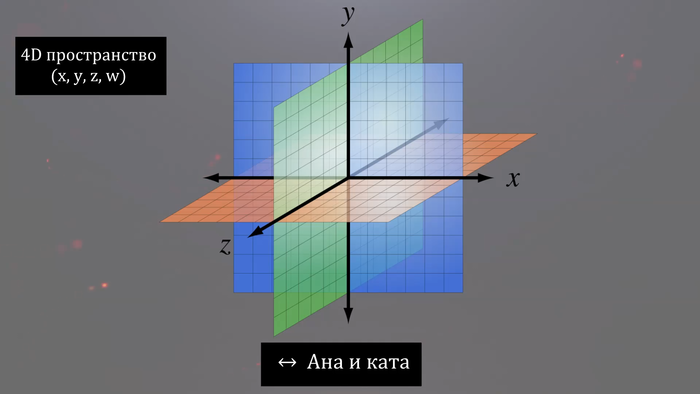
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.
В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.
В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.
Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?
Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.
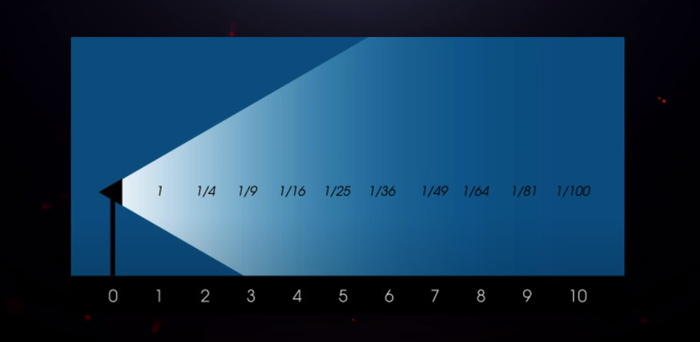
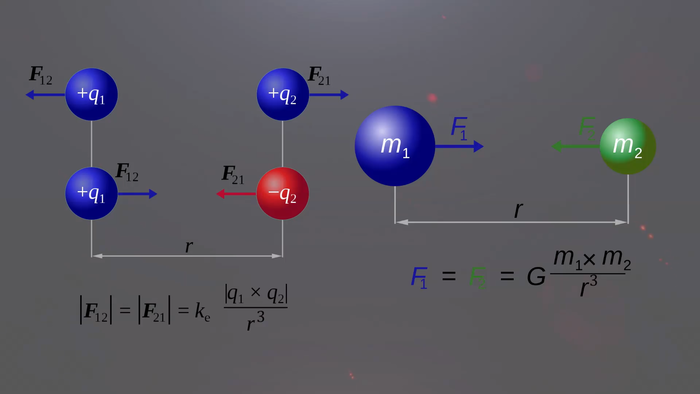
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.
Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.
В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.
Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.
Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.
Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.
Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.
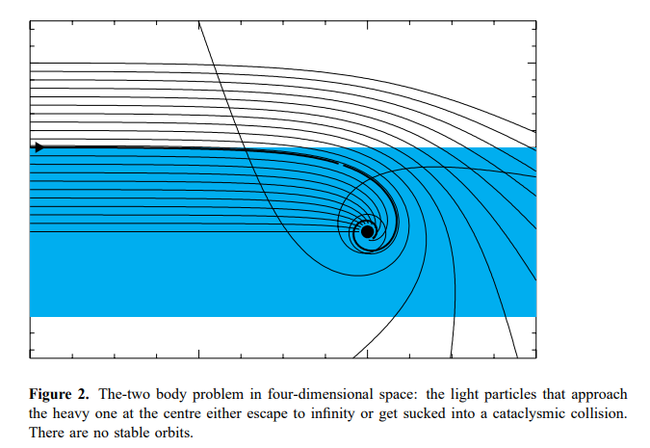
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.
Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.
Книга Кипа Торна, «Интерстеллар. Наука за кадром»
Чёрные дыры и расизм
Корнельский университет США инициировал новый учебный курс: студентам объяснят, являются ли расистскими космические черные дыры. А в качестве приглашенных экспертов выступят темнокожие (!) теоретики, художники и писатели-фантасты.
5 рассказов, закрученных на физике и математике в художественном исполнении
Подборка, совмещающая познавательное с развлекательным. С физическим парадоксами, новыми измерениями, математическими теоремами и интересными сюжетами.
1. «Колодец Лотоса» Александр Петрович Казанцев
«Сквозь стену колодца Лотоса прошли многие, но немногие стали жрецами бога Ра. Думай. Цени свою жизнь. Так советуют тебе жрецы Ра.» (Колодец Лотоса )
Соединение истории и математики, немного шахматных этюдов и возвышенной любви. Но фокус больше на математике и ее практическом применении в художественном обрамлении. А сейчас поподробнее.
Пока математик будет решать задачу методами, известными в XX-ом веке, повествование переносится на четыре тысячи лет назад, в сам древний Египет, где мы увидим как один юноша будет решать задачу, не владея научными знаниями, которые известны математику, а заодно узнаем историю его любви и того, как и почему он вообще попал на испытание.
Возможно, немного специфично и порекомендую не всем, но, если вам нравится историческое, от упоминаний математических задач не хочется лезть на стену, не пугают архаизмы в художественной речи или вам просто любопытно как древний египтянин решил задачку без знаний уравнений и формул, то почитайте.
В моей версии рассказа отсутствовал рисунок, на который ссылаются в тексте, отдельно скину его в комментарии.
Интересный факт: У рассказа есть более расширенная версия «Шахматы на дне колодца», которая более насыщенная шахматами и математикой.
Время чтения: 48 минут
Под какое настроение: почитать художественную математику 🙂
Жанр: Историческая проза
Аннотация: Любовь к прекрасной царице Хатшепсут приводит молодого художника к Колодцу Лотоса — место испытания жрецов Ра. Сможет ли возлюбленный великой царицы решить задачу, ответ на которую знают только сами жрецы?
2. «Новые измерения» («New Dimensions») Уолтер Тевис
«В ту ночь появилась тысяча новых религиозных культов, а тысяча старых провозгласила, что настал День, Который Был Предвещен Издревле.» («Новые измерения»)
Время чтения: 18 мин.
Под какое настроение: потренировать своё пространственное мышление
Жанр: Научная фантастика
Аннотация: Оливер Фарнзуорт изобрёл пятимерный куб. В трёхмерном пространстве он выглядел как 64 отдельных куба, соединённых в конструкцию наподобие креста. При падении конструкция сложилась в единый куб и в одной из его граней открылось отверстие, через которое просматривался какой-то мохнатый затуманенный шарик.
3. «Нульсторонний профессор» («The No-Sided Professor») Мартин Гарднер
«По словам Мебиуса, теоретически не существовало причин, по которым поверхность не могла бы утратить обе свои стороны, то есть, иными словами, стать «нульсторонней» («Нульсторонний профессор»)
Время чтения: 10 мин.
Под какое настроение: под хорошее, удобно свернувшись в тор 😈
Жанр: Научная фантастика
Аннотация: Общество чикагских математиков, работающих в области топологии, носит название «Мёбиус». 17 ноября каждого года они собираются на банкете и приглашают в качестве гостя какого-либо знаменитого тополога. На этот раз им стал профессор Станислав Сляпенарский из Вены. Он намеревался прочесть лекцию на тему: «Нульсторонние поверхности».
4. «Саймон Флэгг и дьявол» («The Devil and Simon Flagg»), Артур Порджес
«— Математика! — в ужасе воскликнул хвостатый. — Вы думаете, у меня было время изучать такие штуки? Я проходил тривиум и квадривиум, но что касается алгебры… Скажите, возмущенно добавил он, — этично ли задавать мне такой вопрос?» (с) Дьявол
Рассказ в доступной форме знакомит с общими положениями великой теоремы Ферма, доказать или опровергнуть которую возьмется сам Дьявол, одолеет ли он математику или математика одолеет его?
Ведь решение теоремы пытались найти многие ученые более 300-от лет.
Дьявол получился относительно добрым, беседы с ним мягкие, атмосфера спокойная, ученная, математику для прочтения знать хорошо не требуется 🙂
Время чтения: 13 мин.
Под какое настроение: ироничное
Аннотация: Математик Саймон Флэгг вызвал дьявола и заключил с ним стандартное соглашение. Математик хотел знать, верна или не верна великая теорема Ферма.
5. «Идеальный тайник» («Time Locker») Генри Каттнер
— Это значит. ты хочешь, сказать, что этот шкаф внутри больше, чем снаружи?
— Парадокс, не так ли? Я думаю, его внутренность находится вообще не в нашем пространстве-времени. («Идеальный тайник» )
Произведение входит в цикл рассказов «Изобретатель Гэллегер» и вызывает желание почитать и остальное из цикла из-за главного персонажа: изобретателя, который подсознательно творит гениальные вещи, но при этом не особо понимает как оно работает и не сильно-то желает углубляться в маттчасть, что и приводит к неожиданностям.
Время чтения: 41 мин.
Под какое настроение: развлечься, отвлечься
Аннотация: Гэллегер изобрел удивительный шкаф — все, что было в него положено, изменяло свою форму и размер. Даже если предмет сразу не умещался в шкаф, он постепенно в него всасывался. Но принцип действия этого шкафа оказался совсем не таким, как думал Гэллегер.
Если вы любите читать книги или О книгах, то предлагаю присоединиться к моему телеграм-каналу, куда я добавляю то, что читаю и, может быть, вы подберете там себе что-то под любое настроение и в любом жанре)
Как просрать все! Любовь. Студент и преподавательница
Решил поделиться.Устал носить в себе. Никому ранее я это не рассказывал. Но.. вот сподобился. Не для рейтинга. Просто. Делюсь.
Имена, названия вузов и некоторые локации – изменены.
Время действия – без малого 30 лет назад.
Ни разу не писатель. Очень много букв. Поехали
Математику и физику я любил с детства, любовь к ней мне привил ещё отец(умер, когда я был в 8м классе) работавший инженером-конструктором. Да так привил, что, когда в третьем классе все писа́ли 2+2, я уже свободно решал линейные уравнения и пытался решать квадратные. Причем это было не по какому-то принуждению, а добровольно и с радостью. Колмогоров был моей настольной книгой. Потом добавились Ландсберг, Торн. Затем первый том Ландау-Лившица(к последним классам). Ещё и с пятого класса взяли в СДЮШОР на плавание. Ходил. Не то чтобы сильно нравилось, но прикольно. До самого конца школы отплавал. Поэтому рос не «задохликом», а довольно крепким парнем. Ещё и рост.. В отца!
Но, страстью моей были математика и физика, они дава́лись мне легко и непринужденно. Поэтому, вопроса: «куда поступать?» не возникало никогда. Только политех, физмат, по стопам отца. Поступил без проблем, само-собой! Высший балл!
И вот! Первая пара по матану. Заходит ОНА. Чуть выше среднего! Худенькая-худенькая)) Строгое платье! Волосы в хвост! Очёчки такие, лисичками)) И глазища! Океан! Ольга Викторовна, доцент кафедры математического анализа, кандидат ф.-м.н. («Мегера», так нас ею пугали). Когда она начала рассказывать про интегралы, ньютоновские «флюксии», геометрический смысл производной, – у нее горели глаза. Да что там глаза! Она вся преображалась и начинала светиться от счастья. Я сразу подумал: «ВОТ ОНО. Вот человек, который болен математикой так же как и я. «.
И я, здоровый 19летний лоб, влюбился в 32летнюю математичку! По уши! А она, походу, увидела в моих глазах тоже самое что и я в ее! То, что она и хотела увидеть в глазах балбесов, с таким воодушевлением рассказывая про свою страсть – математику!
«Вопросы?», в конце. «Будут! Ещё как!», подумал я. Помню остался после занятий, мы долго разговаривали. Обо мне, о математике, о ее докторской, которую она пишет. Мне ее тема была но́во, сложно, а значит – безумно интересно!! Она сидит рядом и что-то говорит, говорит, говорит! Я что-то даже отвечаю, даже вроде в тему, а у самого́ сердце БУМ-БУМ-БУМ и одна мысль пульсирует в голове: «Господи! Как же я тебя ХОЧУ. «.
В течении этого семестра я часто оставался с ней. Чисто поболтать о математике, физике. А она была в восторге от моего неподдельного интереса ко всему этому! Не.. ну пытался конечно отвешивать какие-то неуклюжие комплименты. Иногда удавалось дотронуться до ее руки. Проскакивала такая искра, что вдрагивали оба! Выяснил, что она замужем. За каким-то профессором из Военмеха. Намного старше ее. Расстроился капец! Но детей не было, почему-то..
(Хотел бы заметить, что я это пишу как бы постфактум. В то время, я, молодой балбес, не придавал значения и четверти тех нюансов, которые описываю сейчас!)
И эти мучения продолжались и следующий семестр. Но был и прогресс. Мы уже разговаривали не только о математике, но и о жизни. О ней, обо мне, о планах на будущее (не совместных, естественно). Оказывается ее давно приглашают преподавать в один из европейских вузов. Она – хочет, но муж против. Изредка таки удавалось проводить ее до дома и это было счастье, идти с ней рядом! Да ее тоже тянуло ко мне, я чувствовал, но виду она старалась не подавать. Окружающие замечали, конечно, все это, но, как мне кажется, считали что я просто немного с прибабахом на почве математики(что было не так уж и далеко от истины). Впрочем, её все считали ещё более пое́хавшей(за эту «двинутость» я ее и полюбил), поэтому тот факт что мы постоянно вместе, что-то решаем, обсуждаем и спорим, ни у кого не вызвал удивления. А на па́рах и лекциях, все было строго. Субординация. Только что́, почти не вызывала и ничего не требовала, ибо и так прекрасно знала мой уровень. На ее занятиях и лекциях я подрабатывал, делая курсовые и рефераты для балбесов со старших курсов. И самому интересно и деньги платят. Красота!
Так все и шло. До некоторого момента..
В этот февральский день на кафедре был какой-то сабантуй. Я, если честно, уже точный повод и не помню. То ли юбилей у кого-то, то ли какая-то годовщина кафедры. Я, хм. как «перспективный студент» и вообще, вечно ошивающийся на кафедре кадр, тоже был приглашен. Естественно: тосты, поздравления, какая-то болтовня. Математика, опять же, куда же без нее.
И, само собой, я опять пошел ее провожать. Ещё и чуть винцом подогретый, самую малость. Да и она тоже. У нее сапожки такие.. на каблучках.. тук-тук-тук!))) Было скользко, она взяла меня под руку, а я боялся пошевелить рукой! Как будто спугнуть боялся. Не дышал даже и ног не чувствовал от счастья! Уж не помню о чем мы говорили, но, так уж получилось, что, когда мы дошли до ее парадной, я ее поцеловал. Сам испугался! А она.. а она ответила на поцелуй! Это было восхитительно! Просто непередаваемо! Мы стояли у ее парадной и целовались! Упиваясь друг другом! Задыхаясь! Забыв про все на свете! Про время! Соседей! Мужа!
Я увлёк нас в парадную(в те времена домофонов ещё не было) уже расстегивая на ходу ее пальто и дава́я волю рукам. Вроде бы было чуть слышное: «Не надо..», но.. совершенно неубедительное, да и она тоже, при этом, продолжала целовать и шарила по моей спине! Руки холодные.. мурашки..
Мы любили друг друга в её парадной! На лестнице! На подоконнике! Такой страсти и отдачи я не чувствовал никогда, до этого момента! Она стонала так, что мне приходилось зажимать ей рот, чтобы не поднять на уши весь дом! За что и поплатился прокушенным пальцем)), до сих пор следы! Все мои предыдущие «попытки» заниматься сексом(а их было немало, парень то я видный, в отца, плюс общага..), казались даже не «жалким подобием», а какой-то детской вознёй! Я такого ну просто не ожидал! Даже представить не мог что такое возможно! Это не описать словами!
Когда все закончилось (я понятия не имею сколько времени это длилось! Может час! А может и пару минут!). Так вот, когда все закончилось, она молча поправила одежду, и, поле того как отдышалась, сказала единственное слово: «Уходи» – тихо-тихо, одними губами. Чмокнула в щеку и приложила палец к своим губам, мол: «Все хорошо! Но помалкивай». И ушла..
А я остался стоять и не знал что делать. И был на седьмом небе от счастья.
И ещё.. я снова ее хотел. Нестерпимо!! А впереди были два выходных!! Целая вечность..
А как она меня ревновала, когда я приходил на пары «помятый» после общажных посиделок! О-оо! Моооё почтение! Этот взгляд надо было видеть! Как рентгеновский лазер – невидим для окружающих, но прожигает насквозь! Глупая! Да для меня не существовало никого, только ОНА! И математика!
Мне хотелось взять ее на руки и бегать с ней по институту, крича от радости! Но вместо этого в голову полезла какая-то дебильная хрень: «а что скажут люди?» «Она на 13 лет меня старше», «в общаге засмеют»и т.п. Идиот!
На пары я в тот день не пошел! Сидел в сквере неподалеку. Курил. Одну за одной, накручивая себя из-за этой разницы в возрасте! Как же я себя ненавижу за это.
Дождавшись перерыва, поплелся в сторону кафедры..
И.. нет бы мне ее обнять и расцеловать, после этого! Нифига подобного! Сижу и снова что-то мя́млю про то что, мол «зачем?», «надо подумать», «давай будем как раньше», «мы всё-таки не ровесники» и все в таком духе(((
В итоге она..жёстко так: «зачётка с собой?». Киваю. «На стол!», говорит. Поставила все зачёты и экзамен за второй курс. «Свободен, Коршунов. Чтоб я тебя на своих предметах больше не видела!». Зло́ так говорит!
Психанул! В голове: «Ах! Не хочешь видеть. Ну хорошо!»
Там. Решил что пойду на что-нибудь медицинское. Учил химию, биологию и. пил! Практически не просыхая.
Я заехал к своей матери( мы почти не общались с ней и делами друг друга не интересовались). Она сказала что в конце осени заходила «какая-то худющая баба». Просила повлиять на меня, чтобы я не творил ерунды и не бросал учебу. Мать ответила типа: «Мне плевать, он сам разберётся, но я передам, как явится». Пох. (Дебил!) Уехал обратно. Готовиться к поступлению и бухать.
А в августе умирает моя мать (сердце). Похороны, то-сё!
Сжёг. Пытался забыть. Хрен там! Тогда я успокаивал себя тем, что мол, ничего страшного, у меня вся жизнь впереди, полная приключений(Ога! щаз!). И только лет через десять(!) начал в полной мере осознавать что НА САМОМ ДЕЛЕ я потерял!! Из-за своей дурости и упрямства.
Вот так молодой, «перспективный студент» в одночасье просрал все и всех! И любимую женщину. И любовь к математике. Ребенка!
Кстати, к математике я больше не прикасался ни разу в жизни. Даже смотреть не могу на учебники, не то что прикасаться! К алкоголю, кстати, тоже.
Пс: Ольга Викторовна. Если вдруг. Каким-то чудом вы это прочтёте. Знайте. Я вас любил так как никогда в жизни! Идиот! Говорил совсем не то что на самом деле хотел сказать. И делал совсем не то что на самом деле хотел сделать. Простите меня! Я очень надеюсь что у вас все сложилось хорошо и вы забыли придурка Сашу!