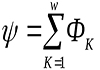индуктивность в чем измеряется в системе си
Калькулятор индуктивности — перевод единиц индуктивности онлайн
В системе единиц СИ индуктивность измеряется в генри, сокращенно Гн. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. В данном обзоре помимо краткого теоретического обзора представлен калькулятор индуктивности для перевода в десятичные приставки в системе СИ.
Индуктивность — теоретические основы
Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.
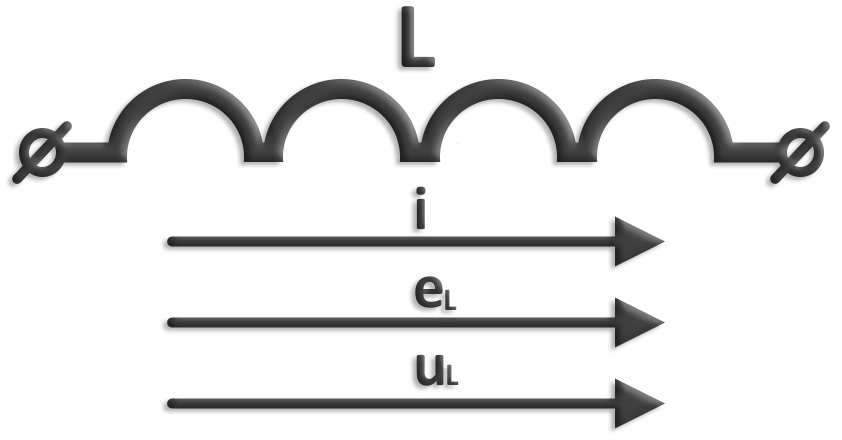
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.
По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током
катушки L=Ψ/i.
Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Поток сцепления катушки индуктивности равен Ψ=L×i.
В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.
Напряжение на индуктивности уравновешивает ЭДС и может быть записано в
виде uL=-eL=dΨ/dt=L×di/dt.
Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.
Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.
Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.
Калькулятор индуктивности онлайн
Калькулятор-конвертер индуктивности позволит быстро перевести Генри в десятичные кратные и дольные единицы.
Индуктивность
Из Википедии — свободной энциклопедии
Индуктивность является электрической инерцией, подобной механической инерции тел. А вот мерой этой электрической инерции как свойством проводника может служить ЭДС самоиндукции. Характеризуется свойством проводника противодействовать появлению, прекращению и всякому изменению электрического тока в нём.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [4] :
E i = − d Φ d t = − L d I d t <\displaystyle <\mathcal
 .
.При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током [4] :
Для имитации индуктивности, то есть ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются [6] и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
Индуктивность
Индуктивность — это коэффициент пропорциональности между электрическом током, проходящим в замкнутом контуре и магнитным потоком, образуемым этим током через поверхность, у которой контур является краем. Индуктивность обозначается символом L, принятым в честь Э.Ленца.
Ф — величина магнитного потока, которая пронизывает контур с 1 витком;
I — величина тока;
L — индуктивность витка;
L — коэффициент пропорциональности между Ф и I.
Если катушка состоит из N витков, то полным потоком (или потокосцеплением) будет сумма магнитных потоков через все витки, тогда
Индуктивность L зависит от размеров, формы проводника, количества витков и т.п., от магнитной проницаемости среды.
Единица измерения в системе СИ названа генри (Гн) в честь Дж.Генри. В Гауссовой системе и СГС, СГСМ системах индуктивность считают в сантиметрах 1 Гн = 1000000000 см, 1 см = 1 нГн. Для сантиметров используют название абгенри.в качестве единицы. В системе СГСЭ единицу индуктивности называют статгенри, либо оставляют без названия.
1 статгенри приблизительно равен 8,987552 х 10 в 11 степени генри.
1 Гн = 1000 Миллигенри
1 Гн = 1000000 Микрогенри
1 Гн = 0,001 Килогенри
1 Гн = 0,000001 Мегагенри
Рассчитать индуктивность и осуществить быстрый перевод единиц измерения можно с помощью онлайн калькулятора.
Генри
Генри.
Генри – единица измерения индуктивности в Международной системе единиц (СИ). Имеет русское обозначение – Гн и международное обозначение – H.
Перевод генри в другие единицы измерения
Другие единицы измерения
Генри, как единица измерения:
Генри – единица измерения индуктивности в Международной системе единиц (СИ), названная в честь американского учёного Джозефа Генри.
Генри как единица измерения имеет русское обозначение – Гн и международное обозначение – H.
Цепь имеет индуктивность в один генри, если изменение электрического тока со скоростью один ампер в секунду создаёт ЭДС индукции, равную одному вольту.
1 генри также равен индуктивности электрического контура, возбуждающего магнитный поток в 1 вебер при силе постоянного тока в нём 1 ампер.
Гн = В · с / А = (кг · м 2 ) / (с 2 · А 2 ) = Вб / А.
1 Гн = 1 В · 1 с / 1 А = (1 кг · 1 м 2 ) / (1 с 2 · 1 А 2 ) = 1 Вб / 1 А.
В Международную систему единиц генри введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы «генри» пишется со строчной буквы, а её обозначение — с заглавной (Гн). Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием генри.
Применение генри:
В генри измеряют индуктивность и взаимную индуктивность проводника.
Представление генри в других единицах измерения – формулы:
Через основные и производные единицы системы СИ генри выражается следующим образом:
Гн = (кг · м 2 ) / (с 2 · А 2 )
Кратные и дольные единицы генри:
Кратные и дольные единицы образуются с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 10 1 Гн | декагенри | даГн | daH | 10 −1 Гн | децигенри | дГн | dH |
| 10 2 Гн | гектогенри | гГн | hH | 10 −2 Гн | сантигенри | сГн | cH |
| 10 3 Гн | килогенри | кГн | kH | 10 −3 Гн | миллигенри | мГн | mH |
| 10 6 Гн | мегагенри | МГн | MH | 10 −6 Гн | микрогенри | мкГн | µH |
| 10 9 Гн | гигагенри | ГГн | GH | 10 −9 Гн | наногенри | нГн | nH |
| 10 12 Гн | терагенри | ТГн | TH | 10 −12 Гн | пикогенри | пГн | pH |
| 10 15 Гн | петагенри | ПГн | PH | 10 −15 Гн | фемтогенри | фГн | fH |
| 10 18 Гн | эксагенри | ЭГн | EH | 10 −18 Гн | аттогенри | аГн | aH |
| 10 21 Гн | зеттагенри | ЗГн | ZH | 10 −21 Гн | зептогенри | зГн | zH |
| 10 24 Гн | иоттагенри | ИГн | YH | 10 −24 Гн | иоктогенри | иГн | yH |
Примечание: © Фото https://www.pexels.com, https://pixabay.com
1 генри единица измерения индуктивности магнитного потока физика формула перевод единиц
единицей измерения какой физической величины является 1 генри
единицей си магнитного потока является генри гн
Что такое единица измерения индуктивности в системе СИ?
хотя, почему индуктивность измеряется в Генри?
Не менее важно, что такое единица измерения конденсатора в системе СИ?
иначе Что такое единица измерения вязкости в системе СИ?
Что такое индуктивность XL? Формула:
Как рассчитывается Л. Генри?
Какая буква используется для обозначения тока?
Ток измеряется в амперах, обозначается значком буква «я». Сопротивление измеряется в Ом и обозначается буквой «R».
Какая формула конденсатора?
Какие бывают три типа конденсаторов?
Что такое конденсатор?
Какая жидкость имеет самую высокую вязкость?
Какая единица измерения вязкости в системе СИ * 2 балла?
Размеры динамической вязкости: сила × время ÷ площадь. Единицей вязкости, соответственно, является ньютон-секунда на квадратный метр, который обычно выражается в паскаль-секунде в единицах СИ.
Почему вязкость измеряется в паскалях в секундах?
Что такое XC и XL?
Как найти индуктивность XL?
Формула для расчета индуктивного сопротивления катушки: индуктивное реактивное сопротивление, или XL, является произведением удвоенной p (пи), или 2, частоты переменного тока в герцах и индуктивности катушки в генри. XL =2 p xfx L. L = значение индуктивности катушки в генри.
Каковы значения XL и XC в DC?
Частота постоянного тока равна 0. Итак, в цепи постоянного тока. Если есть индуктор (XL будет 0), отсутствие импеданса означает, что это идеальный проводник, ведущий к короткому замыканию. Что касается емкостного реактивного сопротивления, XC бесконечен для DC что означает обрыв цепи.
Что такое препарат Генри?
(Британия, сленг) Количество марихуаны весом одну восьмую унции.
Как рассчитывается индукция?
Формула для расчета индуктивного сопротивления катушки: индуктивное реактивное сопротивление, или XL, является произведением удвоенной p (пи), или 2, частоты переменного тока в герцах и индуктивности катушки в генри. XL =2 p xfx L. L = значение индуктивности катушки в генри.
Как сделать индуктор 1 генри?
Теоретически это один наноуглерод, вращающийся вокруг миллионов раз создаст 1 индуктор Генри, даже мега индуктор Генри. Вот индуктор с воздушным сердечником и воздушным сердечником, который вы можете легко сделать. Индуктивность этой катушки индуктивности может достигать 1 Генри, если увеличить количество витков.
Какие 7 частей буквы?
Эксперты в целом сходятся во мнении, что деловое письмо состоит из семи основных частей:
Какие 5 частей дружеского письма?
Личные письма, также известные как дружеские письма, и социальные заметки обычно состоят из пяти частей.
Какие бывают 3 типа писем?
В общем, обычно используются 3 основных типа букв:
Что такое формула индуктора?
VT V =1 + V2 +V3. Мы знаем, что напряжение на катушке индуктивности определяется уравнением. V = L di / dt.
Почему конденсаторы блокируют постоянный ток?
Мы знаем, что в источнике постоянного тока нет частоты, то есть частоты 0 Гц. Если мы поместим частоту «f = 0» в формулу индуктивного реактивного сопротивления (которое является сопротивлением переменному току в емкостной цепи). Если положить XC как бесконечность, значение тока будет равно нулю. Это точная причина, по которой конденсаторный блок постоянного тока.