что нельзя делать в математике
Урок 7. Устранение проблем с математикой

Беря это во внимание, мы решили, что поговорить о трудностях с математикой с точки зрения педагогики и психологии будет вполне уместно. Несмотря на то, что практической информации, как таковой, в уроке минимум, в общем и целом эти знания непременно пригодятся вам на практике. Причем полезны они будут не только во время ваших занятий с ребенком, но и в перспективе – когда он пойдет в школу, начнет делать уроки, быть может, выбирать программу с углубленным изучением каких-то предметов.
Итак, давайте приступим.
Содержание:
Трудности с математикой
Изучая математику, с проблемами сталкивается огромное количество детей. Если числа, таблица умножения и простейшие вычисления даются всем, то формулы, доказательства теорем и тригонометрические функции может осилить не каждый. Однако от уроков и школьной программы деваться некуда, а это значит, что познавать азы необходимо. Чего же может не хватать детям, чтобы подружиться с царицей наук?
Множеству родителей знакомы проблемы их детей с алгеброй и геометрией. Уроки делаются всем семейством, а сам процесс нередко сопровождается истериками, нервами, стрессами и усталостью, отчего математика становится настоящим бичом, а уроки – серьезным испытанием на прочность. В итоге мамы и папы ломают голову над тем, какую помощь оказать ребенку: и чтобы предмет давался легче, и чтобы каждая неудовлетворительная оценка в тетрадке не становилась причиной для плохого настроения или – что часто случается – слез.
Математику можно смело назвать одним из самых спорных предметов в школьной программе, и среди выпускников всегда можно найти тех, у кого одни пятерки по всем дисциплинами, но только не по математике. Родители же в свою очередь относятся к такого рода проблемам по-разному. Одни уверены в том, что математика очень важна, а потому чуть ли не силой заставляют свое чадо грызть гранит науки, даже если он действительно не по зубам. Другие, видя в ребенке проявления гуманитарного склада ума, считают, что главное – это успехи в литературе, русском и иностранных языках, истории и т.д., а с математикой – да бог с ней, с этой математикой.
Но следует ли сводить на нет важность этого предмета, даже если в малыше уже с ранних лет наружу пытается выбраться творческая натура? К категории творческих людей можно отнести писателей, поэтов, художников, а также историков, журналистов и редакторов. Но если, например, художнику или писателю математика на самом деле нужна постольку-поскольку, то в таких профессиях, как журналист, историк или редактор она все-таки пригождается. Математика – это основа системного мышления, и во многих областях жизнедеятельности человека без нее не обойтись.
Когда у детей возникают трудности с математикой, родители часто говорят: «Ну не понимает он (или она) этого предмета, нет у него предрасположенности к нему». В итоге не остается ничего, кроме того чтобы без ропота принять сложность математики. «Зато остальные предметы даются ребенку прекрасно!». Однако, по мнению опытных педагогов и профессиональных репетиторов по математике (например, Леонида Костюкова) этот предмет может быть значительно проще остальных. Фишка в том, что математика – наука последовательная, и нет никакой необходимости заучивать бесчисленное количество дат, терминов и понятий. Все, что требуется от ученика – это понять математику.
Кроме того, если ребенок хорошо осваивает языки, каких бы то ни было проблем с освоением математики у него просто быть не должно. Большая часть иностранных языков построена на вполне логичной и понятной структуре, а школьная программа по изучению английского языка гораздо сложнее программы по изучению математики. Картинка, согласитесь, рисуется довольно приятная, но почему на деле все не так?
Психология «отношений» ребенка и математики
Профессиональные психологи (к примеру, детский психолог Елена Морозова) указывают на то, что между детьми, хорошо соображающими в технических дисциплинах, и остальными детьми есть некоторые психологические отличия. По большому счету, дети, любящие математику, характеризуются любопытством, готовностью пойти на риск, настойчивостью, отсутствием страха перед трудностями. А те, у кого с математикой «ни то, ни се», часто отличаются неуверенностью в себе, зависимостью от мнения родителей и других окружающих людей, боязнью трудностей, а также убежденностью в том, что они не так сообразительны, как остальные. Потому-то и решение трудных математических задач вызывает серьезные затруднения.
Вышеназванные различия формируются еще в детском садике и начальных классах школы. Одни дети умеют хорошо читать, а другие что-то невнятно мямлят. Одни знают таблицу умножения, а другие с трудом складывают «17» и «15». Одни при счете перебирают пальчики, а другие с успехом демонстрируют абстрактно-образное мышление. Одним не стоит никакого труда представить, как первый поезд выходит из пункта A, а второй – из пункта B, и встречаются они в точке C, а для других это – фантастика.
Все это во множестве случаев является следствием отсутствия фундамента математической дисциплины, по причине чего ребенку гораздо легче вообще запустить математику, нежели постараться в ней разобраться.
Любая запущенная математическая трудность лишь усугубляет проблемы в будущем. А в литературе, например, подобные проблемы отсутствуют, т.к. если ученик не читал «Отцы и дети» И. С. Тургенева, это совсем не мешает ему прочитать «Войну и мир» Л. Н. Толстого. С математикой же такое не прокатит, ведь из-за какой-то теоремы, непонятой в пятом классе, начнутся проблемы в последующих классах.
Но, по мнению все тех же психологов, отсутствие успеха в изучении математики может быть связано не только со способностями, но и с эмоциональными особенностями детей. Во-первых, и сами родители не всегда проявляют чудеса педагогики и воспитания, занимаясь ранним развитием своих подопечных, а во-вторых, не каждый учитель – Учитель с большой буквы. Особенности воспитания и стиль преподавания играют огромную роль и накладывают свой отпечаток. В частности, если ребенку часто дают понять, что он чего-то не соображает, отстает, не способен понять «прописных истин», на положительные результаты обучения рассчитывать не стоит.
Есть ли у родителей выход?
Нет совершенно никаких сомнений в том, что детские трудности с математикой, особенно когда они наблюдаются в старшем дошкольном и младшем школьном возрасте, воспринимаются родителями отнюдь не радостно. Но критика и злость по отношению к ребенку нисколько не облегчают ситуацию. И, опять же, психологи в этом вопросе сходятся – родители ни в коем случае не должны нагнетать обстановку, а, наоборот, должны стараться снимать напряжение, вызванное математикой. Нельзя фокусировать внимание ребенка на неудачах и отсутствии успеха. Если что-то не получается, это вполне можно исправить.
Не заставляйте ребенка зазубривать через силу основы предмета. С математикой ваша маленькая драгоценность сможет справиться только в том случае, если вы сможете донести целостность этой дисциплины. Старайтесь подводить свое чадо к самостоятельным решениям, как можно доступнее объясняя моменты, мешающие ему понять и увидеть – как решается пример, задача или уравнение. Если же желание научить ребенка основам математики есть, а возможности заниматься с ним самим по каким-то причинам нет, есть смысл прибегнуть к услугам репетитора. Но он должен не только разбираться в своем предмете, но и иметь опыт работы с детьми.
Но давайте резюмируем все вышесказанное, чтобы разложить все по полочкам.
Почему возникают проблемы с математикой
Не забывайте, что в этом уроке мы обсуждаем проблемы с математикой с психологической точки зрения. Исходя из этого, основными причинами таких проблем являются:
Имейте в виду, что эти причины относятся к основным. Разбирая математические трудности ребенка, нужно брать в расчет наличие индивидуальных психологических проблем, зачастую совершенно не связанных с интеллектуальным потенциалом.
Что делать родителям
Подходя к вопросу решения проблем с математикой профессионально, следует прибегать к следующим методам:
Проблемы у детей с математикой – это не нечто из ряда вон выходящее; они есть всегда и везде. Например, несколько лет назад, американское издание New York Times (выпуск от 28 июля 2014 года) поднимало вопрос о том, нужна ли вообще ученикам алгебра, если каждый четвертый американский школьник не может получить аттестат из-за «неприятностей» с математикой. А министр образования и науки Франции Клод Аллегрэ, будучи сам ученым-физиком, дискутировал на тему исключения математики из школьной программы, ссылаясь на то, что множество детей не способны решить даже элементарные задачи. Однако дисциплина все так же остается одной из главных в школе, а для многих – и в жизни.
Но помните, что умение считать, знание таблицы умножения, хорошие оценки и т.д. – все это прекрасно, но у ребенка могут быть свои потребности и цели. Если один хочет стать новым Пифагором, то для другого важно, чтобы его любили, ценили и принимали таким, какой он есть, а также чтобы математика не вызывала у него страхов и тревог, даже если он чего-то недопонимает. Так что успех вашего чада – в ваших руках. Используйте это ему во благо.
Предпоследний урок блока по обучению детей счету посвящен теме привития ребенку любви к математике. Из него вы узнаете, что делают многие родители, чтобы отбить у малыша всякую охоту осваивать математические основы, и что следует предпринимать, чтобы этого избежать, и чтобы интерес к этой науке возрастал с каждым днем.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
 alisarin
alisarin
alisarin
«Математический запрет»
Далее мне понравились комментарии типа:
в школьном учебнике сказано, что a^0=1 для всех а не равных нулю, а 0^0 не имеет смысла, так же как нельзя делить на ноль. В дальнейшем в курсе матанализа в теории пределов разрешен и 0^0 и деление на 0, но ответ зависит от вида функции, предел которой вы считаете
для leonid: x^0 имеет в нуле точку устранимого разрыва, и можно доопределить ее до непрерывной, но это вовсе не значит, что 0^0=1, тогда получается, что и х/x в нуле равна 1 :))
Ежели играем на поле действительных чисел, то никак низзя. Скажем, ищем массу, это величина действительная, и после умножения на «i» получится хрень на постном масле 🙂
А полного списка нет по той простой причине, шо в математике все, что не разрешено, то запрещено 🙂 Бесконечный список получится 🙂
[ скажем, определить «отношение больше на комплексных числах» ]
Ну возьми да определи, например, можно сравнивать по модулю.
логические запреты
Мне кажется, что тут ответ лежит на поверхности. Математика работает с любыми вещами, которые не ведут к логическому противоречию. Даже можно и противоречивые теории рассматривать, но там выводимы все утверждения, и поэтому они неинтересны.
К тому же надо понимать, что многие вещи являются не «истинами», а соглашениями. Примером может служить то же самое 0^0. Такое выражение можно не разрешать, а можно разрешать, считая его равным 1.
Re: логические запреты
Re: логические запреты
Re: логические запреты
Во-первых, разрешите приветствовать таких редки читателей на этих страницах :))
Называя «абстрактную алгебру», ты сразу окунаешь читателя в бездну:
«Множество есть многое, мыслимое нами как единое» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).
Существует два подхода к понятию множества.
Первый — так называемая «наивная теория множеств» (созданная Кантором, см. ниже историю). Дать определение чему-либо — это значит выразить понятие через ранее определённые. При этом должны быть некоторые базовые понятия, которые формально не определены. Множество — как раз одно из таких понятий. В рамках наивной теории множеств множеством считается любой чётко определённый набор объектов (элементов множества). Вольное использование наивной теории множеств приводит к некоторым парадоксам.
Такова картина, которую можно найти в нечто «Википедия» (мне почему-то кажется, что математический комментарий там весьма недурный); а может быть, все же, попытаться определиться с «множеством» и всем на нем основывающимся.
Решение неравенств: основные ошибки и полезные лайфхаки
Вы умеете решать неравенства? Уверены?
Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.
При решении неравенств мы можем:
1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.
При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.
2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны
3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.
Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.
4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).
5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.
Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.
1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.
2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.
Как, например, решить неравенство
Перенесем все в левую часть неравенства, чтобы в правой остался ноль.
Разложим левую часть на множители.
Запомним: ответы типа « > » абсурдны.
4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.
5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.
6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.
7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.
При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.
Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.
А теперь – полезный лайфхак для решения дробно-рациональных неравенств.
Продолжаем упрощать левую часть:
Теперь можно и привести дроби к одному знаменателю.
Все, больше ничего не пишем. Решаем неравенство методом интервалов.
Пять удивительных математических фактов
Для начала небольшой спойлер 
Да я знаю, что если написать фамилию с заглавной буквы, казуса не получится. Дальше перевод.
Математика – одна из немногих областей знаний, которая может быть объективно названа истинной, потому что ее теоремы основаны на чистой логике. Но в то же время эти теоремы часто оказываются очень странными и противоречащими интуиции.
Некоторые люди считают математику скучной. Следующие примеры показывают, что она какая угодно, но не такая
5. Случайные наборы данных

Как это ни странно, случайные данные на самом деле не такие уж и случайные. В приведенных данных, представляющих собой все от биржевых курсов до населения городов, высот зданий и протяженностей рек, около 30 процентов всех чисел начинаются с единицы. Меньшее количество начинается с 2, еще меньше с 3 и так далее, с 9 начинается только каждое двадцатое число. И чем больше набор данных, чем шире порядок охватываемых величин, тем сильнее проявляется эта закономерность.
4. Спирали простых чисел
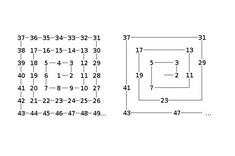
В силу того, что простые числа неделимы (кроме как на единицу и самого себя), и того, что все остальные числа могут быть представлены в виде их произведения, простые числа часто рассматриваются как «атомы» в мире математики. Несмотря на свою важность, распределение простых чисел до сих пор остается тайной. Нет такого правила, которое бы однозначно говорило, какие числа будут простыми и через сколько встретится следующее простое число.
Кажущаяся случайность простых чисел делает факты, обнаруженные в «Скатерти Улама» очень странными.
В 1963 году математик Станислав Улам, обнаружил удивительную закономерность, когда разрисовывал свою записную книжку во время презентации: если записывать целые числа по спирали, простые числа выстраиваются вдоль диагональных линий. Само по себе это не очень удивительно, если помнить, что все простые числа, кроме двойки, нечетные, а диагональные линии в спиралях целых чисел поочередно являются нечетными. Более необычной была тенденция простых чисел лежать преимущественно на одних диагоналях и практически отсутствовать на других. Причем закономерность наблюдалась вне зависимости от того, с какого числа начиналась спираль (с единицы или любого другого).
Даже если масштабировать спираль, чтобы она вмещала гораздо большее количество чисел, можно увидеть, что скопление простых чисел на одних диагоналях гораздо плотнее, чем на других. Существуют математические предположения, объясняющие эту закономерность, но пока они не доказаны.
3. Выворачивание сферы
В одной важной области математики, которая называется топология, два объекта считаются эквивалентными или гомеоморфными, если один из них может быть преобразован в другой путем скручивания или растягивания поверхности. Объекты считаются разными, если для преобразования требуются разрезы или изломы поверхности.
В качестве примера рассмотрим тор – объект в форме пончика. Если поставить его вертикально, расширить одну сторону и вдавить верхушку этой же стороны, то получится цилиндрический объект с ручкой. В среде математиков существует классическая шутка, что топологи не могут отличить пончика от чашки с кофе.
С другой стороны, ленты Мебиуса – петли с единственным перегибом не являются гомеоморфными петлями без перегибов (цилиндры), потому что нельзя распрямить ленту Мебиуса, без того чтобы разрезать ее, перевернуть одну сторону и склеить заново.
Топологов давно интересует вопрос, будет ли сфера гомеоморфной самой себе, будучи вывернутой наизнанку? Другими словами, можно ли выворачивать сферу? На первый взгляд это кажется невозможным, потому что нельзя проткнуть дырку в сфере. Но, оказывается, выворачивание сферы возможно. Как это делается, показано на видео
.
Поражает тот факт, что тополог Бернард Морин, который является главным разработчиком приведенного метода выворачивания сферы, слеп.
2. Математика стен

Несмотря на то, что стены могут быть украшены бесконечным количеством завитушек, говоря математическим языком, существует конечное число отдельных геометрических шаблонов. Все периодические рисунки Эшера, обои, плиточные дизайны и вообще все двумерные повторяющиеся группы фигур, могут быть отнесены к той или иной так называемой «плоской кристаллографической группе». И знаете, сколько существует таких групп? Ровно 17.
1. Сонет

«Как сонет Шекспира схватывает саму суть любви, или картина показывает внутреннюю красоту человека, уравнение Эйлера проникает в самые глубины существования.»
Математик из Стэнфорда Кейт Девлин (Keith Devlin) написал эти слова об уравнении в эссе 2002 года, которое называлось «Самое прекрасное уравнение». Но почему от формулы Эйлера перехватывает дыхание? И что она вообще значит?
Во-первых, буква «e» представляет собой иррациональное число (с бесконечным количеством цифр), которое начинается с 2.71828… Открытое в контексте непрерывно начисляемого сложного процента, оно описывает темпы экспоненциального роста от колоний популяций насекомых до радиоактивного распада. В математике число обладает рядом неожиданных свойств, например, оно равняется сумме обратных факториалов от нуля до бесконечности. В конечном счете константа e оккупировала математику, взявшись вроде бы ниоткуда, но оказавшись в большом числе важных уравнений.
Далее. i представляет собой так называемую мнимую единицу – квадратный корень из минус 1. «Так называемую», потому что в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число (потому отрицательные числа не имеют действительных квадратных корней). Но в математике существует большое количество ситуаций, когда приходится извлекать квадратный корень из отрицательного числа. Число i используется как своеобразная пометка того места, где такая операция была произведена.
Пи – отношение длины окружности к ее диаметру, одна из любимых и наиболее интересных констант в математике. Подобно e, она появилась в большом количестве математических и физических формул как будто из ниоткуда.
Константа e, возведенная в степень мнимая единица, умноженная на Пи равняется минус одному. Из уравнения Эйлера следует, что добавление к этому единицы дает ноль. Трудно поверить, что все эти странные числа, одно из которых даже не относится к реальному миру, могут быть так просто скомбинированы. Но это доказанный факт.
Математика в жизни: где нужна и как избежать
«Зачем мне эта ваша математика? Где она мне в жизни пригодится?» Разбираемся.
Катя Павловская для Skillbox Media
Этому дерзкому вопросу, по всей видимости, столько же лет, сколько математика вообще преподаётся. Ещё совсем недавно школьные учителя и вузовские преподаватели любили отвечать на него линейкой по лбу цитатой из Ломоносова про то, что якобы она, математика, «ум в порядок приводит».
К слову, эта знаменитая фраза со школьных плакатов, скорее всего, не является подлинной, а приписана Михаилу Васильевичу автором книги «История арифметики» И. Я. Депманом в 1959 году. Менее (или более) верной она от этого, конечно, не становится.
В наше время основной ответ прост: с математикой человек больше зарабатывает. Так, в рейтингах самых высокооплачиваемых профессий стабильно присутствуют финансисты и айтишники, а эти отрасли насквозь пронизаны разнообразной математикой.
Про «самую сексуальную профессию XXI века» яснее любых слов скажет старый мем.
Но что, если вы не алчный айтишник ищете своё призвание в медицине, искусстве, литературе, юриспруденции, дизайне, психологии или развлечениях? Насколько нужна будет вам математика в этом случае? Возможно ли вообще избежать встречи с ней?
Спойлер-1: да, возможно.
Спойлер-2: в какой-то момент, вероятно, станет проще её таки изучить.
Кандидат философских наук, специалист по математическому моделированию. Пишет про Data Science, AI и программирование на Python.
В быту
Где нужна. Математика — в виде элементарной арифметики — в повседневной жизни пригодится для расчёта:
Начала геометрии (площади и объёмы простых фигур) потребуются, когда вы будете подсчитывать количество необходимых материалов для ремонта в доме. Более продвинутая математика (функции и сложные проценты) нужна, если вы оцениваете стоимость кредита, лизинга или решаете, куда вложить свободные средства.
Как избежать. В наши дни все перечисленные и многие другие задачи совершенно не обязательно решать самому. В смартфонах есть калькуляторы, а в интернете, App Store и Google Play — сайты и приложения для расчёта чего угодно: рецептов, финансов, тренировок и путешествий.
Для покупки отделочных и строительных материалов вам нужно просто сказать продавцу размеры комнаты, дома или участка. Если вы инвестируете, то в вашем личном кабинете на сайте банка или брокера уже есть готовые решения на любую стратегию.
Приложения, сервисы и специально обученные люди считают точнее и быстрее, чем вы. Реально, вам даже таблицу умножения можно неделями не вспоминать, если не месяцами. Сколько там будет 7 × 9? …Всё! — математическая программа на неделю выполнена.
Что изучить, если не избегать. Устный счёт — например, систему Трахтенберга или ментальную арифметику. Площади треугольника, прямоугольника, круга, объёмы параллелепипеда, пирамиды, цилиндра, конуса, шара. Теорему Пифагора и формулу Герона. Формулу сложных процентов и начало курса про финансовые рынки на сайте Академии Хана.
Кроме «Википедии» и учебников для начальной и средней школы, можно прочитать классические книги Я. И. Перельмана по занимательной арифметике и математическим головоломкам. Если захочется чего-то посложнее, посмотрите книгу Сергея Самойленко про математику повседневной жизни.
В учёбе
Где нужна: для написания контрольных, получения зачётов и сдачи экзаменов. В России математика преподаётся даже на самых гуманитарных направлениях в школах и вузах, где зачастую скромный объём программы с лихвой компенсируется атмосферой всеобщего трепета перед ней.
Парадокс: заговора математиков по проникновению во все отрасли не существует, но математика тем не менее повсюду.
В литературоведении арифметика нужна для выяснения стихотворного размера, а статистический анализ текста используется для определения авторства. Музыкальное образование начинается со счёта для развития чувства ритма, а художественное — с рисования простейших геометрических фигур.
В социальных науках математика помогает понять связи или корреляции между площадью и населением, выраженными в числах, и ситуацией в регионе или стране. Письменный перевод (лингвистическая дисциплина) уже стал разделом компьютерных наук и, в своей теоретической части, математики.
Формулы классической логики, которая является краеугольным камнем философского и юридического образования, прочно связаны как с математической теорией множеств, так и с булевой алгеброй, лежащей в основе современных компьютеров.
Как избежать. Полностью уклониться от математики в учёбе, скорее всего, не получится, так что встречайте неизбежное с полагающимся самураю достоинством. Тем не менее снизить вероятность совсем уж хардкорного хардкора можно следующими путями:
Международный день математики — 14 марта, он же День числа пи. Неофициальный День математика в университетах нашей страны отмечается 1 апреля (не спрашивайте почему). Математикам не дают Нобелевскую премию — учтите это, если будете сочинять преподавателю поздравление с этими праздниками.
Что и как изучить. Преподаватели, и не только математики, весьма чувствительны даже к малейшим признакам неуважения к своему предмету. Поэтому от вас требуются собранность, дисциплина и прилежание — или как минимум их убедительная видимость.
Будьте осторожны со шпаргалками из интернета — как правило, преподаватели знают их все наизусть. К тому же бездумное заучивание не даёт понимания — а того, кто не понимает, о чём говорит, на экзамене видно сразу. Соответственно, риск дополнительных вопросов → стыд-позор-провал → пересдача.
Лучше всего потратить время на нормальное освоение темы — на основе тех же шпаргалок, — а также на знакомство с дополнительной литературой. Например, можно прочитать бестселлер Стивена Строгаца «Удовольствие от x»: автор обещает нам ни больше ни меньше «второй шанс для знакомства с математикой».
Для карьеры
Где нужна. Даже если ваша работа не связана с математикой напрямую, она может содержаться под капотом в разных инструментах типа формул и макросов в Excel или скриптов для анимации в After Effects.
Второй способ применения математики в карьере — это решение задач на собеседованиях, курсах повышения квалификации, профессиональных конкурсах и сертификационных экзаменах. Сюда относятся, начиная с самых распространённых:
Наконец, третий способ применения математики на работе — символический, когда важно не знание математики, а интерес к ней. Например, если гендир окончил мехмат МГУ, то руководителем департамента скорее станет тот, кто понимает (или старается понять) его шутки про матан и топологию.
Как избежать. Математика в рабочих инструментах спрятана глубоко, и обычному пользователю, как правило, недоступна и не нужна. Поэтому достаточно изучить инструкцию и освоить основные практические приёмы.
Для удовлетворительного решения тестов на IQ тоже можно обойтись без специального изучения математики. Здесь поможет обычный здравый смысл и, главное, опыт решения именно этого типа задач, которые в большинстве восходят к оригинальным тестам Айзенка.
Прочитайте разбор этих задач, сделанный академиком В. Васильевым, а также статью про силлогизмы, особенно часть про круги Эйлера.
Задачи с подвохом, не имеющие точного ответа, решаются с помощью вычисления Ферми. Это метод приближённой оценки чего угодно, основанный на имеющихся у вас знаниях о проблеме. Такие задачи призваны выявить не столько знание математики, сколько кругозор кандидата, его уверенность и способность рассуждать.
Наконец, для того чтобы понимать математиков, можно просто попросить объяснить. Коллеги тоже люди, им нравится чувствовать себя умными и образованными. Зачем-то же, в конце концов, они учились на мехмате?!
Что изучить, если хотите изучить. Решение квадратных уравнений и неравенств. Основные функции: линейная, квадратичная, кубическая, показательная, логарифмическая, тригонометрические. Их производные и интегралы. Начала комбинаторики и теории вероятностей.
Также обратите внимание на курсы в Skillbox, например «Excel + Google Таблицы с нуля до PRO».
Упражняться в решении тестов можно по сборникам вроде «Большой книги IQ-тестов» Ф. Картера и К. Рассела. Общую эрудицию — знание географии, биологии, истории, литературы — подтяните с помощью базы вопросов «Что? Где? Когда?». Ответы и ссылки на источники там есть.
Хорошие темы для small talk с коллегами, идентифицирующими себя как математиков, — это история, философия и методы этой науки. Книг на эту тему великое множество, посоветуем три и одну статью:
В 1960 году физик Юджин Вигнер написал статью «Непостижимая эффективность математики в естественных науках». Одно название ласкает слух любого математика («непостижимая»!), а идеи оттуда можно обсуждать часами — они, к слову, до сих пор звучат очень современно.
Например, гипотеза о связи сознания и квантовых процессов, развитая позднее физиком Роджером Пенроузом в книге «Новый ум короля».
Для хобби и саморазвития
Тем, кто увлекается ставками на исходы спортивных событий, не повредит знакомство с теорией вероятностей и математической статистикой. Базовая статистика нужна и для тайм-менеджмента, основанного на учёте и анализе потраченного времени.
Вообще, теория вероятностей — это один из наиболее практичных способов войти в математику. Главное, чему она учит:
Теорема Байеса, математическая индукция, закон больших чисел и другие методы решения самых разнообразных задач, которые даёт нам математика, лежат в основе рационального мышления, способствуют осознанности и, в конечном итоге, улучшают качество нашей жизни.
Книги, которые можно прочитать, начиная с самых доступных:
Для всего
Мыслить как математик — это значит уметь обобщать и моделировать. Это основы абстрактного мышления, а «использование правильных абстракций приводит к более глубокому проникновению в суть вопроса и большему могуществу при его решении» (С. Строгац, «Удовольствие от x»).
Абстрактное мышление является нашим эволюционным преимуществом — мы умеем с пользой для себя обращаться с тем, что невозможно учуять, увидеть или попробовать на зуб.
Теорикрафтинг (от англ. theorycrafting) — подбор оптимальной экипировки, расчёт урона, «оттачивание» и балансирование персонажа компьютерной игры с использованием специальных калькуляторов, формул и таблиц.
Макс Тегмарк — шведско-американский космолог и астрофизик, профессор MIT. Автор популярной книги «Наша математическая вселенная».
 alisarin
alisarin






