что называют шагом квантования
Что называют шагом квантования
Цифровые аудио сигналы
Компьютер – это цифровое устройство, то есть электронное устройство, в котором рабочим сигналом является дискретный сигнал. Сегодняшние компьютеры оперируют дискретными сигналами, несущими двоичные значения, условно обозначаемые как «да» и «нет» (на электрическом уровне: 0 вольт и V вольт, для некоторого ненулевого значения V). С помощью одного двоичного сигнала за один шаг можно передать информацию об одном из всего двух положений: 0 («да») или 1 («нет»). С помощью N двоичных сигналов за один шаг можно передать информацию об одном из 2 N положений (2 N – это число комбинаций нулей и единиц для N сигналов). Взаимодействие всех составляющих компьютер блоков происходит путем обмена и обработки одним или одновременно несколькими двоичными сигналами. Все – коды управления, а также сама обрабатываемая информация – все представляется в компьютере в виде чисел. По этой причине и аудио сигналы в цифровой аппаратуре представляют в виде чисел.
Дискретизация
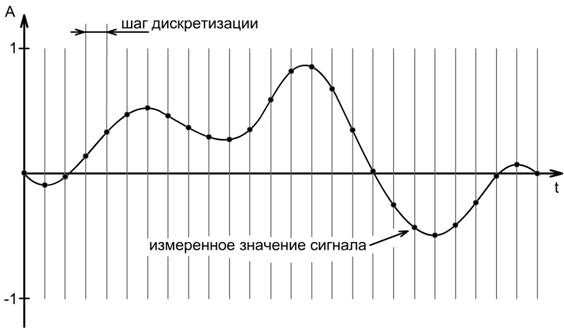
Количество осуществляемых в одну секунду замеров величины сигнала называют частотой дискретизации или частотой выборки, или частотой сэмплирования (от англ. « sampling» – «выборка») . Очевидно, что чем меньше шаг дискретизации, тем выше частота дискретизации (то есть, тем чаще регистрируются значения амплитуды), и, значит, тем более точное представление о сигнале мы получаем. Это рассуждение подтверждается доказанной теоремой, теоремой Котельникова (в зарубежной литературе встречается как теорема Шеннона, Shannon). Согласно этой теореме, аналоговый сигнал с ограниченным спектром может быть точно описан дискретной последовательностью значений его амплитуды, если эти значения следуют с частотой, как минимум вдвое превышающей наивысшую частоту спектра. Иначе говоря, аналоговый сигнал, в котором частота наивысшей составляющей спектра равна F m, может быть точно описан последовательностью дискретных значений амплитуды, если для частоты дискретизации F d выполняется: 
. На практике это означает следующее: для того, чтобы оцифрованный сигнал содержал информацию о всем диапазоне слышимых человеком частот исходного аналогового сигнала (0 – 20 кГц) необходимо, чтобы выбранное значение частоты дискретизации при оцифровке сигнала составляло не менее 40 кГц.
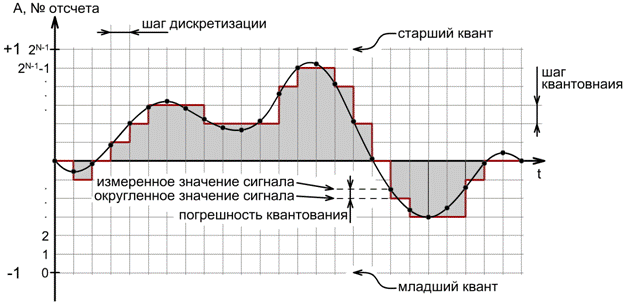
Линейное (однородное) квантование
Как видно, результатом такой оцифровки стал ступенчатый сигнал, составленный из прямоугольников, каждый из которых имеет ширину равную величине шага дискретизации, и высоту равную измеренному значению амплитуды сигнала.
Сложности, связанные с оцифровкой
Не смотря на кажущуюся простоту и интуитивность процесса оцифровки, эта процедура сопряжена со многими трудностями и проблемами.
Во-первых, частота дискретизации, устанавливаемая теоремой Котельникова, является минимально необходимой, но не достаточной. Дискретизация вносит дополнительные помехи в спектр исходного сигнала, добавляя в него его же зеркальную копию. Поэтому значение частоты дискретизации должно выбираться несколько б о льшим, чем частота, устанавливаемая теоремой Котельникова, чтобы сделать возможной успешную фильтрацию лишних спектральных составляющих.
Надо сказать, что уровень шума квантования также зависит и от формы самого сигнала. В идеальном случае, ошибка при округлении значений сигнала является случайной и, значит, спектр шума квантования оказывается равномерным. В реальности, однако, этого не происходит. Форма реальных звуковых сигналов является в определенной степени не случайной, а, значит, и ошибка квантования тоже является не случайной. В этом случае спектр шума квантования оказывается не равномерным и концентрируется в какой-то определенной области, что отрицательно сказывается на звучании цифрового сигнала. Существует несколько способов борьбы с этим явлением. Так, нежелательную концентрацию шума квантования в некоторой частотной области можно нейтрализовать путем подмешивания к исходному аналоговому сигналу некоторого слабого по мощности псевдослучайного шума. Этот шум минимизирует степень зависимости ошибок округления от формы преобразуемого сигнала, что хорошо рассеивает спектр шума квантования и делает его равномерным. Таким образом, описанный прием (называемый дизерингом, от англ. « dithering» – «дрожание») как бы подменяет нежелательный шум квантования искусственно подмешанным псевдослучайным шумом. При этом подмешанный псевдослучайный шум оказывается менее заметным на слух, чем тот шум квантования, какой получился бы без применения дизеринга. Еще один прием борьбы с уровнем шума квантования называется формовкой шума (от англ. “ noise shaping”). Идея приема заключается в преднамеренном изменении формы исходного аналогового сигнала специальным образом, чтобы последующее квантование привело к появлению шума квантования, основная энергия которого расположилась бы в наименее заметных на слух частотных областях. Формирование шума с таким спектром достигают путем использования фильтра, моделирующего кривую равной громкости (об этой кривой мы говорили выше).
Импульсный сигнал, получаемый в результате аналогово-цифрового преобразования, из-за несовершенности преобразующих устройств имеет некоторые изъяны. Эти изъяны выражаются в случайных отклонениях длительностей прямоугольных импульсов от номинальной величины шага дискретизации, а также в неабсолютной крутизне фронтов импульсов. Говоря иначе, осуществление выборки сигнала при оцифровке происходит не через абсолютно равные промежутки времени, а с некоторыми случайными отклонениями от номинала, при этом результирующий импульсный сигнал вдобавок имеет неидеальную прямоугольную форму. Если, скажем, дискретизация проводится с частотой 44.1 кГц, то отсчеты берутся не точно каждые 
секунды, а то чуть раньше, то чуть позднее. А так как входной сигнал постоянно меняется, то такая погрешность приводит к регистрации не совсем верного уровня сигнала. Описанный неприятный эффект называется джиттером (от англ. « jitter» – «дрожание») и по сути является исключительно результатом неабсолютной стабильности аппаратуры (АЦП). На слух джиттер воспринимается как некоторое дрожание сигнала на высоких частотах, при этом на низких частотах джиттер выражается в некотором «размазывании» спектра сигнала. Для борьбы с джиттером применяют высокостабильные тактовые генераторы. Следует заметить, что причиной появления джиттера может быть не только аналогово-цифровое преобразование, но и передача импульсного сигнала по цифровому каналу от одного устройства к другому. В этом случае появление джиттера является результатом неидеальной коммутации/синхронизации устройств и может быть устранено только путем использования аппаратуры, регенерирующей цифровой сигнал.
Цифровое представление аналогового аудиосигнала. Краткий ликбез
Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.
Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.
Чем отличается цифровой аудиосигнал от аналогового?
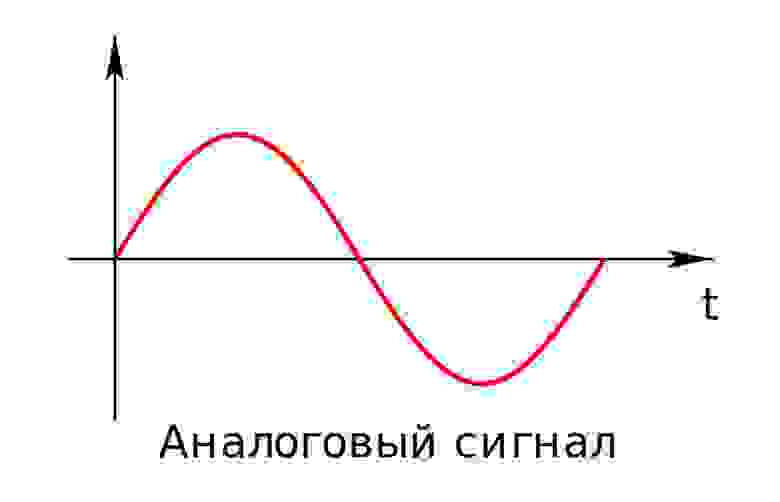
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).
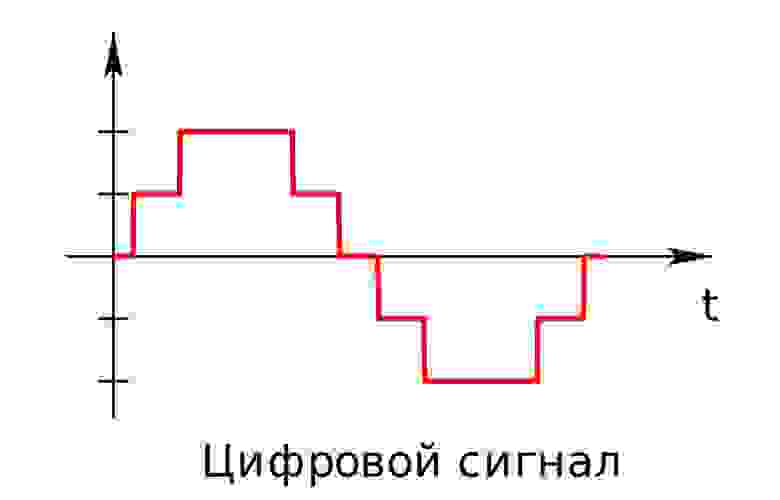
Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).
Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).
Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).
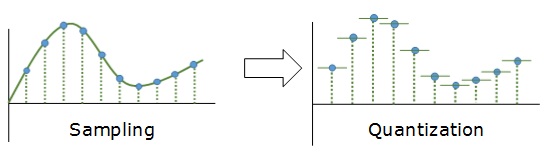
Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).
Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
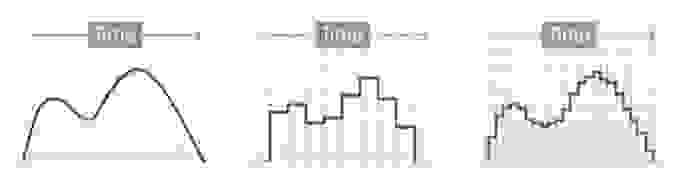
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).
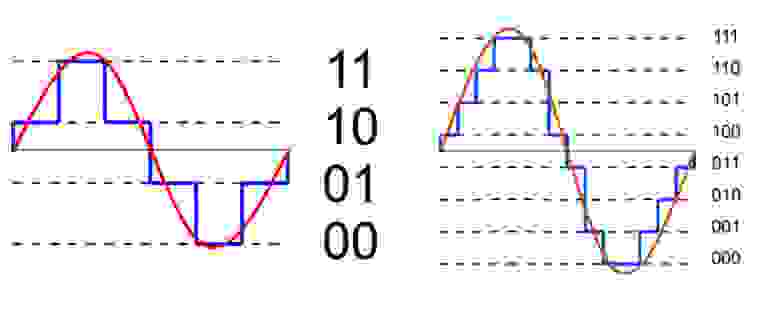
Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)
Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).
Данная формула позволяет вычислить количество уровней квантования:
Если N — количество уровней квантования,
n — разрядность, то
Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.
При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.
Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением 
и квантованным значением 
(
)
Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).
Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).
Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).
Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.
50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.
Теперь о дискретизации.
Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то 
Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).
Теорема Котельникова гласит:
Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.
Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.
Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?
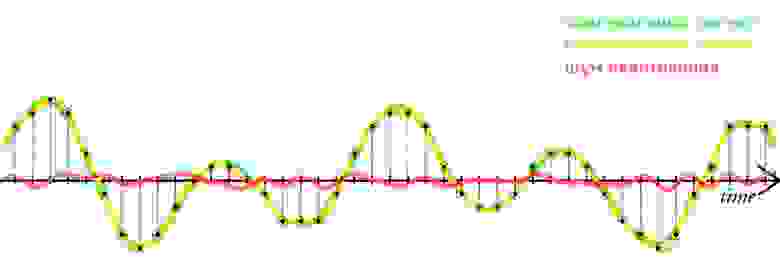
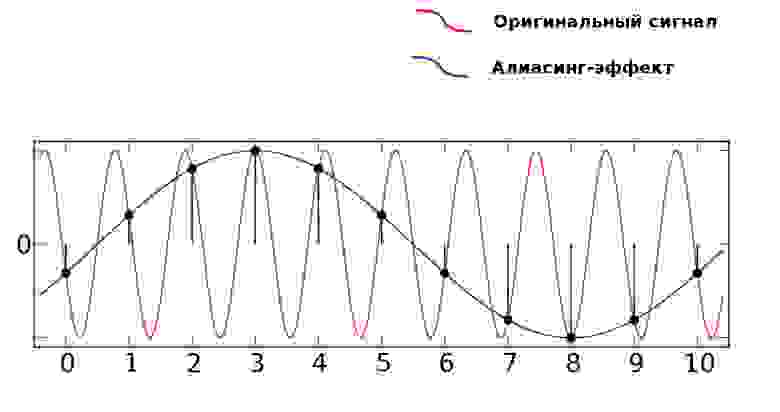
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.
Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.
Аудиопример 4: Линейно возрастающая частота от
100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.
Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг
Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.
Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.
Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):
Битрейт = Частота дискретизации * Разрядность * Количество каналов
Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s
При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.
При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.
Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.
При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.
ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.
Существуют 3 метода хранения цифрового аудиоматериала:
Несжатый (RAW) формат данных
Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.
Аудиоформаты с сжатием без потерь
Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.
Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.
Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).
Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…
При сжатии с потерями
акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».
Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.
Этим и пользуется кодек: 2kHz-звук можно убрать.
Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…
Дискретизация
Дискретизация – переход от непрерывного сигнала к близкому (в определенном смысле) дискретному сигналу, описываемому разрывной функцией времени. Пример дискретного сигнала – последовательность коротких импульсов с изменяющейся амплитудой (последняя выступает в данном случае в качестве информативного параметра).
Обработка и передача дискретной информации имеет ряд преимуществ по сравнению с информацией, заданной в непрерывном виде. Дискретные сигналы в меньшей степени подвержены искажениям в процессе передачи и хранения, они легко преобразуются в двоичный цифровой код и обрабатываются с помощью цифровых вычислительных устройств.
Процесс дискретизации состоит обычно из двух этапов: дискретизации по времени и дискретизации (квантования) по уровню.
Дискретизация аналогового сигнала по времени – процесс формирования выборки аналогового сигнала в моменты времени, кратные периоду дискретизирующей последовательности ∆t.
Дискретизирующая последовательность – периодическая последовательность отсчетов времени, задающая сетку дискретного времени.
Период дискретизации ∆t – интервал времени между двумя последовательными отсчетами аналогового сигнала (шаг дискретизации по времени).
При выборе частоты дискретизации по времени можно воспользоваться теоремой В.А. Котельникова.
Теорема отсчетов (теорема Котельникова) – теорема, определяющая выбор периода дискретизации ∆t аналогового сигнала в соответствии с его спектральной характеристикой.
Согласно теореме, всякий непрерывный сигнал, имеющий ограниченный частотный спектр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга на интервалы времени ∆t = l/(2Fmax), где Fmax – максимальная частота в спектре сигнала. Иначе, дискретизация по времени не связана с потерей информации, если частота дискретизации f дискр = 1/∆t в два раза выше указанной верхней частоты сигнала Fmax.
Согласно теореме Котельникова, нет необходимости передавать бесконечное множество всех значений непрерывного сигнала x(t), достаточно передавать лишь те его значения (рис. 3.52), которые отстоят друг от друга на расстоянии ∆t = l/(2Fmax). Для восстановления сигнала x(t) на вход идеального фильтра низких частот, имеющего полосу пропускания частот от 0 до Fmsx, необходимо подать последовательность узких импульсов с амплитудой, соответствующей дискретным отсчетам сигнала x(ti) в моменты времени ti = i ∆t.
Рис. 3.52. Дискретные отсчеты сигнала
Поскольку теорема отсчетов (теорема Котельникова) сформулирована для сигнала с ограниченным спектром, а реальные сигналы имеют неограниченную спектральную плотность, то при расчетах ∆t =1/(2Fmax) используют приближенное значение Fmax (например, активную ширину спектра, определенную по амплитудному критерию, по критерию 90%-ного содержания энергии или средней мощности сигнала). Кроме того, и идеальный фильтр низких частот, необходимый для восстановления сигнала в соответствии с теоремой, является физически нереализуемым, так как предъявляемые к нему требования (идеально прямоугольная форма амплитудно-частотной характеристики, отсутствие фазового сдвига в рассматриваемой полосе частот от 0 до Fmax) оказываются противоречивыми и могут выполняться лишь с определенной погрешностью. Учитывая сказанное, частоту дискретизации по времени обычно принимают в 1,5–2,5 раза больше значения, рассчитанного по теореме Котельникова.
Существуют и другие способы выбора частоты дискретизации сигнала (с учетом времени корреляции передаваемого сообщения, значения наибольшего или среднеквадратичного отклонения процесса). Так, в соответствии с критерием Н.А. Железнова, который выполняется для случайных сигналов, имеющих конечную длительность Тс и неограниченный частотный спектр, рекомендуется принимать шаг дискретизации ∆t, равный максимальному интервалу корреляции сигнала φ0. Предполагается, что параметр φ0, характеризует такой промежуток времени, в пределах которого отдельные значения случайного процесса можно считать статистически зависимыми (коррелированными), причем φ0Тс. Таким образом, исходный непрерывный сигнал заменяется совокупностью N=Тс/φ0 некоррелированных отсчетов (импульсов), следующих с частотой fдискр=1/∆t= φ0. При этом восстановление сигнала x(t) осуществляется с помощью линейного прогнозирующего фильтра со среднеквадратической ошибкой, сколь угодно мало отличающейся от нуля в промежутке времени, равном интервалу корреляции φ0.
Более полно учитывая свойства реальных сигналов (конечная длительность, неограниченность спектра), критерий Железнова тем не менее исходит из допущения о равенстве нулю корреляционной функции сигнала Кх(φ) вне интервала [-φ0; φ0], что на практике выполняется с определенной погрешностью.
В тех случаях, когда имеется более подробная информация о законе изменения сигнала, выбор частоты дискретизации можно осуществлять исходя из допустимой погрешности аппроксимации функции x(t) на каждом из интервалов дискретизации. На рис. 3.53 дан пример кусочно-линейной аппроксимации, когда соседние отсчеты функции x(t), взятые в дискретные моменты времени ti и ti+1, соединяются отрезками прямых.
Рис. 3.53. Кусочно-линейная аппроксимация
Рассмотренные способы равномерной дискретизации (при ∆t=const) иногда могут приводить к получению избыточных отсчетов, не оказывающих существенного влияния на процесс восстановления исходного сообщения. Например, если функция x(t) мало изменяется на некотором, достаточно протяженном интервале времени То, то соответствующие дискретные отсчеты сигнала практически не отличаются друг от друга и, следовательно, нет необходимости использовать все указанные отсчеты для хранения или передачи информации по линии связи. Сокращение избыточной информации возможно на основе способов адаптивной (неравномерной) дискретизации, обеспечивающих выбор интервала ∆t между соседними отсчетами с учетом фактического изменения характеристик сигнала (в частности скорости его изменения).
Дискретизация сигнала по уровню – процесс отображения бесконечного множества значений аналогового сигнала на некоторое конечное множество (определяемое числом уровней квантования).
Шаг квантования – величина, равная интервалу между двумя соседними уровнями кванто-вания (определена только для случая равномерного квантования).
Необходимость квантования вызвана тем, что цифровые вычислительные устройства могут оперировать только с числами, имеющими конечное число разрядов. Таким образом, квантование представляет собой округление передаваемых значений с заданной точностью. При равномерном квантовании (∆x=const) число разрешенных дискретных уровней х составляет
где xmax и xmin – соответственно верхняя и нижняя границы диапазона изменения сигнала.
Ошибка квантования – величина, определяемая как ξ(х) = х – хдi, где х – кодируемая дискретная величина, хдi– дискретизированный сигнал.
Шум квантования – случайная функция времени, определяемая как зависимость ошибки квантования от времени.
Если функция x(t) заранее неизвестна, а шаг квантования ∆х достаточно мал по сравнению с диапазоном изменения сигнала (хmax – хmin), то принято считать ошибку квантования ξ(х) случайной величиной, подчиняющейся равномерному закону распределения. Тогда, как показано на рис. 3.54, плотность вероятности f1(ξ) для случайной величины ξ, принимает значение 1/(∆х) внутри интервала (-∆х/2; +∆х/2) и равна нулю вне этого интервала.
Рис. 3.54. Равномерный закон распределения ошибки квантования
При ∆x=const относительная погрешность квантования ∆х=ξ(х)/х существенно зависит от текущего значения сигнала x(t). В связи с этим при необходимости обработки и передачи сигналов, изменяющихся в широком диапазоне, нередко используется неравномерное (нелинейное) квантование, когда шаг ∆х принимается малым для сигналов низкого уровня и увеличивается с ростом соответствующих значений сигнала (например ∆х выбирают пропорционально логарифму значения |x(t)|). Выбор шага ∆хi =хдi – хдi-1 осуществляется еще и с учетом плотности распределения случайного сигнала (для более вероятных значений сигнала шаг квантования выбирают меньшим, для менее вероятных – большим). Таким образом удается обеспечить высокую точность преобразования при ограниченном (не слишком большом) числе разрешенных дискретных уровней сигнала x(t).
Процесс преобразования дискретного сигнала в цифровой называют кодированием информации, а множество различных кодовых комбинаций, получаемых при данном правиле кодирования, – кодом. Важной характеристикой кода является основание (или значность) кода, т.е. число возможных значений, которые могут принимать элементы кодовой комбинации. Пусть требуется передать сигнал, уровень которого изменяется от 0 до 10 В. Если шаг квантования данных составляет 10 мВ, то каждый отсчет сигнала можно рассматривать как одно из 1000 возможных сообщений. Для передачи этой информации можно предложить различные способы:
– каждому сообщению поставить в соответствие определенный уровень напряжения, при этом основание кода m = 1000, а длина кодовой комбинации (слова) принимает минимальное значение n=1;
– можно воспользоваться двоичным (бинарным) представлением амплитуды сигнала с m = 2, но тогда потребуется комбинация длины n = 10 (210=1024, так что некоторые комбинации здесь не использованы).