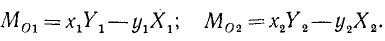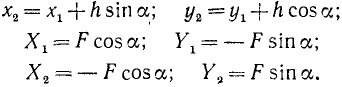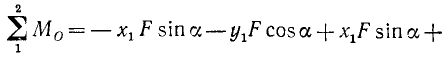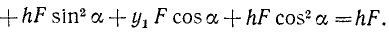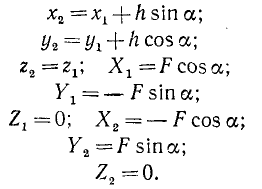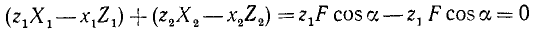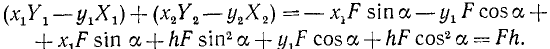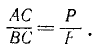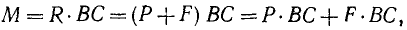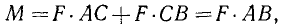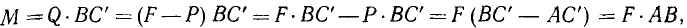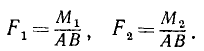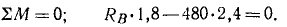что называют парой сил

Техническая механика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

5. Пара сил. Момент силы

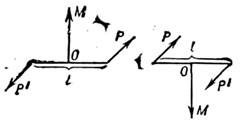
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.

Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом. Силы, входящие в пару, не уравновешиваются, так как они приложены к двум точкам.

Действие этих сил на тело не может быть заменено одной равнодействующей силой.

Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил плеча пары

Конец ознакомительного фрагмента.

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

Смотрите также

Сопротивление материалов. Шпаргалка для студентов

Роман Сиренко, 2009

Анализ финансовой отчетности. Шпаргалки

Группа авторов, 2010

Курс подготовки судоводителей маломерных судов

Коллектив авторов, 2019

Рабочая программа по спортивной радиопеленгации для групп высшего спортивного мастерства

Евгений Головихин, 2010

Движение и зависание топлива в бункерах

Электрический конденсатор. Полная описательная теория принципа работы. Русский вариант

Солнечное вещество и другие повести, а также Жизнь и судьба Матвея Бронштейна и Лидии Чуковской (сборник)

Матвей Бронштейн, 2018

Атлас Новых Профессий. Энергогенерация и накопление энергии. Профессии, которые появятся до 2030 года

Татьяна Александровна Тонунц

Структура мироздания Вселенной. Часть 1. Микромир

Александр Александрович Шадрин

Брайан Китинг, 2018

Новости науки. Исследования на кухонном столе

Технологии управляемого прямого синтеза. Введение

Источник

Теоретическая механика

9. Плоская система сил. Пара сил. Момент пары сил.

Плоская система сил

Система сил, действующих на плоскости, называется плоской системой сил. Особенностью плоской системы сил заключается в том, что линии действия этих сил уже не пересекаются в одной точке.

Одним из важнейших понятий плоской системы сил является понятие пары сил.

Парой сил называется система двух, равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Согласно аксиоме №1 пара сил не находится в равновесии и не имеет равнодействующую.

Вычисление алгебраического момента пары сил. Для вычисления алгебраического момента пары сил, удобно воспользоваться результатом следующей теоремы.

Теорема. Алгебраическая сумма моментов сил, составляющих пару, относительно любого центра, лежащего в плоскости действия пары сил не зависит от выбора этого центра. Момент пары сил равен произведению одной из сил, составляющих пару на плечо пары.

Пусть в плоскости действует пара сил, как показано на рис.С.24.

Тогда, согласно определению алгебраического момента пары сил и в соответствии с правилом знаков для момента силы относительно центра можно записать

Таким образом, алгебраический момент пары сил не зависит от расстояния до центра и равен произведению модуля силы на плечо пары.

Что и требовалось доказать.

В дальнейшем необходимо рассмотреть следующие теоремы, выражающие основные свойства пар сил и устанавливающие условие эквивалентности двух пар сил.

Теорема. Две пары сил, лежащие в одной плоскости и имеющие численно равные моменты и одинаковое направление вращения, эквивалентны.

Доказательство теоремы проведем в несколько этапов.

4. Согласно теореме Вариньона

Из доказанной теоремы вытекают два важных следствия.

Следствие 1. У данной пары сил, не изменяя оказываемого действия, можно менять величину и направление сил, а также длину плеча, сохраняя при этом величину момента силы.

Следствие 2. Данную пару сил, не изменяя оказываемого действия, можно переносить куда угодно в плоскости действия пары. Следовательно, действие пары на тело не зависит от положения пары в ее плоскости. Таким образом, момент пары является свободным вектором!

Источник

ПАРА СИЛ

Расстояние l между линиями действиясил пары наз. плечом П. с. Действие, оказываемое П. с. на твёрдое тело,

Полезное

Смотреть что такое «ПАРА СИЛ» в других словарях:

Пара сил — Пара сил две равные по величине и противоположные по направлению силы, приложенные к одному телу. Равнодействующая пары сил нулевой вектор. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары.… … Википедия

ПАРА СИЛ — две равные по величине и противоположные по направлению параллельные силы, приложенные к одному телу. Пара сил не имеет равнодействующей. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары. Действие пары… … Большой Энциклопедический словарь

ПАРА СИЛ — две равные и параллельные силы, направленные в противоположные стороны. П. С., действующая на какое нибудь тело, вызывает вращение этого тела вокруг оси, перпендикулярной к плоскости, в которой находится пара сил. Самойлов К. И. Морской словарь.… … Морской словарь

пара сил — пара сил; пара Система двух параллельных сил, равных по модулю и направленных в противоположные стороны … Политехнический терминологический толковый словарь

ПАРА СИЛ — две равные по абсолютному значению и противоположно направленные параллельные силы, приложенные к одному твёрдому телу. П. с. стремится вызвать вращение тела, к которому она приложена, и не имеет (см.) силы. Расстояние между линиями действия П. с … Большая политехническая энциклопедия

ПАРА СИЛ — ПАРА СИЛ, две равных и противоположно направленных параллельных силы. Их действие приводит к возникновению вращательного момента … Научно-технический энциклопедический словарь

пара сил — Две компланарные параллельные силы, равные по величине и противоположные по направлению, приложенные к твёрдому телу на некотором расстоянии друг от друга [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] EN couple… … Справочник технического переводчика

пара сил — две равные по величине и противоположные по направлению параллельные силы, приложенные к одному телу. Пара сил не имеет равнодействующей. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары. Действие пары… … Энциклопедический словарь

ПАРА СИЛ — две равные по а6с. значению (модулю) и противоположные по направлению параллельные силы F и F (см. рис ). прилож. к одному и тому же твёрдому телу. Кратчайшее расстояние l между линиями действия сил пары наз. её плечом. П. с. стремится вызвать… … Большой энциклопедический политехнический словарь

Источник

Пара сил в теоретической механике

Пара сил:

Парой сил называют систему двух численно равных параллельных сил, направленных в противоположные стороны

Пара сил и ее момент. Равнодействующая двух не равных по модулю параллельных сил, направленных в противоположные стороны, равна их разности. Если же такие силы по модулю равны, то они не имеют равнодействующей. Они и не уравновешивают друг друга, за исключением того частного случая, когда они имеют одну общую линию действия. Систему двух численно равных параллельных сил, приложенных к одному телу и направленных в противоположные стороны, называют парой сил.

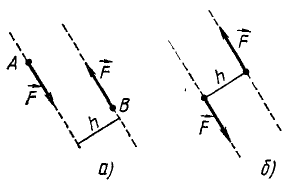
Пусть на тело (рис. 39, а) действует пара сил, причем одна из сил пары приложена в точке А, а другая в точке В. (Тело на рисунке не показано.) Назовем плечом пары кратчайшее расстояние (длину перпендикуляра) между линиями действия сил пары. Сила является скользящим вектором, поэтому силы пары (или одну из них) можно перенести в такое положение (рис. 39, б), чтобы на чертеже отрезок, соединяющий точки их приложения, был перпендикулярен линиям действия сил, т. е. изображал бы плечо.

Плоскость, в которой лежат линии действия сил пары, называют плоскостью пары.

Механическое воздействие пары сил на твердое тело зависит не только от величины сил, но в равной степени также и от плеча. Поэтому за меру механического воздействия пары сил на твердое тело принимают момент пары—величину, численно равную произведению модуля силы на плечо пары:

Момент пары, подобно моменту силы относительно точки,— векторная величина. Вектор момента пары перпендикулярен плоскости пары. Но у всякой плоскости имеется две стороны. Условились вектор момента восставлять с той стороны, с которой пара представляется поворачивающей свое плечо против хода часов (рис. 40). Таким образом, вектор момента пары сил характеризует не только величину воздействия пары на тело, но также и плоскость пары и направление, в котором силы пары стремятся повернуть тело.

В частном случае плоской системы сил момент пары рассматривают как алгебраическую величину и считают положительным, если силы пары стремятся повернуть плечо против вращения стрелок часов, если же силы пары стремятся повернуть плечо по ходу часов, то момент считают отрицательным (рис. 41).

Сумма моментов двух сил пары относительно любой точки пространства равна моменту пары

Свойства пары

Чтобы лучше пояснить понятие пары сил—одно из важнейших понятий механики, покажем, что момент пары сил равен сумме моментов двух сил пары относительно произвольно взятой точки. Для упрощения доказательства мы предположим сначала, что эта точка находится в плоскости пары, а затем распространим теорему на любую точку.

В плоскости пары возьмем совершенно произвольно какую-либо точку О, примем ее за начало плоской системы координат (рис. 42, а), проведем через нее в произвольном направлении ось Ox и перпендикулярно к ней ось Оу. По формуле (16) определим моменты сил пары относительно этой точки О, выбранной нами произвольно и принятой за начало координат:

Но, как видно из чертежа (рис. 42, б),

Подставляя эти величины и складывая, определим сумму моментов двух сил лары относительно точки О:

Таким образом, сумма моментов двух сил пары относительно любой точки О, взятой на ее плоскости, не зависит от их относительного положения (расстояния и ориентации) и равна моменту пары. Отсюда мы можем сделать вывод, что момент пары сил не изменится, если эту точку заменить какой-либо другой или если пару перенести в любое другое место ее плоскости, или повернуть на любой угол в ее плоскости.

Рассмотрим теперь самый общий случай, т. е. не будем накладывать никаких ограничений на положение пары сил и центра моментов. Примем произвольно взятую точку О (рис. 42, в) за начало прямоугольной системы координат, проведем плоскость хОу параллельно плоскости пары, направим оси Ox и Oy произвольно в этой плоскости, а ось Oz-перпендикулярно к ней. Тогда координаты точек приложения сил пары и проекции сил на оси выразятся равенствами, подобными только что написанным, лишь с добавлением третьей координаты, и мы будем иметь:

Учитывая написанные значения координат и проекций сил, определим по (23) суммы моментов двух сил пары относительно координатных осей. Относительно оси Ox получим

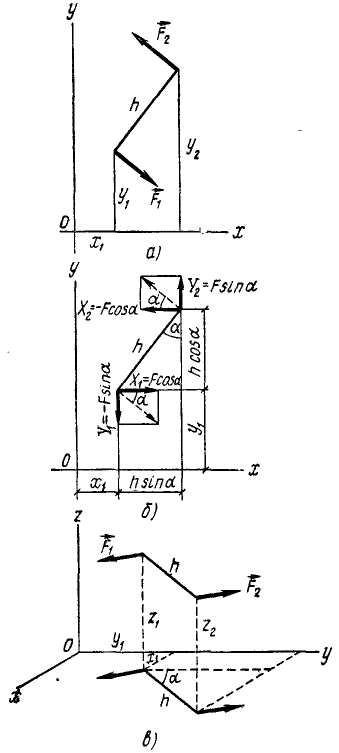
Рис. 42

Аналогично относительно оси Oy

и относительно оси Oz

Теперь по формуле (22) находим, что модуль вектора суммы моментов двух сил пары относительно произвольно взятого центра О равен произведению модуля силы пары на плечо пары. Направлен этот вектор по оси Oz, т. е. перпендикулярно к плоскости пары сил.

Мы убедились, что сумма моментов двух сил пары относительно точки О равна моменту пары вне зависимости не только от положения пары в ее плоскости, но также и от расстояние плоскости пары от центра моментов. Иными словами, момент пары не изменится, если пару перенести в параллельную плоскость.

Момент пары выражается свободным вектором, перпендикулярным к плоскости пары, численно равным произведению силы на плечо

Как уже было сказано, момент пары является мерой механического воздействия пары сил на тело, а потому механическое воздействие пары сил на твердое тело не изменяется, если эту пару поворачивают в ее плоскости, переносят в другое место плоскости или в параллельную плоскость.

Эти на первый взгляд парадоксальные свойства пары поясним примерами. Гаечный ключ (рис. 43) одинаково действует на гайку, к каким бы граням этой гайки его ни приложить — момент пары не изменится от поворота пары сил в ее плоскости. Трансмиссионный вал (рис. 44) сообщает шкиву вращающий момент независимо от места закрепления шкива на валу — момент пары не изменится от переноса пары в параллельную плоскость.

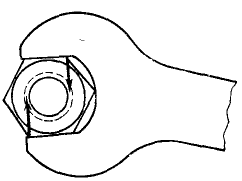Рис. 43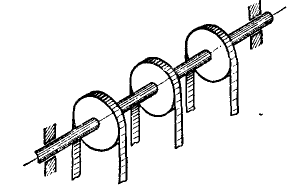

Рис. 44

Но только при изучении динамики, после знакомства с инерцией вращающегося тела и с понятием главных центральных осей, когда читатель узнает, что вращение тела зависит от массы каждой частицы тела и от их распределения, ему станет совершенно ясно, почему Действие пары сил на тело не зависит от положения пары сил в ее плоскости.

Момент пары сил не имеет фиксированной, определенной точки приложения. Он является свободным вектором, т. е. он имеет свою величину и свое направление, но приложить его можно в любой точке твердого тела, на которое действует пара сил. В этом заключается принципиальное отличие момента пары от момента силы относительно точки, являющегося прикрепленным вектором, приложенным в центре момента, или от скользящего вектора, примером которого является сила.

Две пары сил с равными моментами эквивалентны

Эквивалентность пар

Обратим особое внимание на то, что момент пары не является только произведением, а есть мера, полностью характеризующая воздействие пары сил на твердое тело. Две пары с одинаковыми моментами оказывают на тело одинаковое действие, если даже силы одной пары (а также и плечо) не равны силам (и плечу) другой пары.

Докажем сначала, что данную пару (F₁F₂), модули сил которой F, а плечо AB (рис. 45, а), можно, не изменяя ее механического воздействия на твердое тело (тело на рис. 45 не показано), заменить другой парой с таким же моментом, но с большими силами и соответственно меньшим плечом.

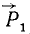
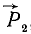
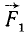
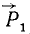
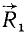
Приложим к телу в точке В, как показано на рис. 45, б, две взаимно уравновешенные силы и , по модулю равные Р. Складывая параллельные силы и , направленные в одну сторону, найдем их равнодействующую , по модулю равную F+P, направленную в ту же сторону и приложенную в точке C на расстояниях AC и ВС, обратно пропорциональных модулям слагаемых сил (рис. 45, в)

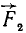
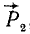
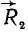
Складывая силы и , приложенные к телу в точке В, получим их равнодействующую , по модулю равную F+P и направленную в сторону слагаемых сил.

Новую пару сил (R₁R₂) мы получили из данной пары (F₁F₂), присоединив к ней взаимно уравновешенные силы P₁ и P₂. Следовательно, обе пары эквивалентны. Момент новой пары равен

т. е. моменты эквивалентных пар равны между собой и данную пару мы заменили другой парой с тем же моментом, но с меньшим плечом.

Чтобы убедиться, что всякую пару сил (F₁F₂) можно заменить другой парой сил с тем же моментом, но с большим плечом и соответственно с меньшими силами, сложим (см. рис. 45, б) силы F₁ с P₂, F₂ с P₁. Мы получим новую пару (Q₁Q₂) (рис. 45, г) с моментом

что и требовалось доказать.

Момент пары сил, полученной от сложения нескольких пар, равен сумме моментов слагаемых пар.

Сложение пар

Покажем, что несколько пар, приложенных к твердому телу, эквивалентны одной паре, момент которой равен сумме их моментов. Пусть к некоторому телу приложены две пары сил, одна из которых лежит в плоскости l и имеет момент M₁, а другая — в плоскости ll и имеет момент M₂. Для общности доказательства предположим, что эти плоскости не пересекаются под углом δ. Воспользовавшись только что доказанными свойствами пар, представим каждую данную пару парой, ей эквивалентной, лежащей в той же плоскости и имеющей плечо AB (рис. 46), расположенное по линии пересечения обеих плоскостей. Модули сил F₁ первой пары и F₂—второй определим из условия эквивалентности

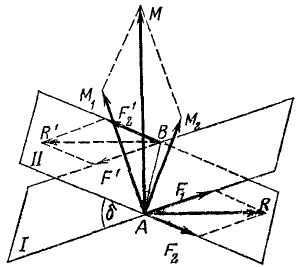
Рис. 46

Сложим силы обеих пар, приложенные к телу в точке А, а затем сложим силы, приложенные в точке В. Получим два параллелограмма сил с вершинами в точках А и В. Эти параллелограммы равны между собой, так как попарно равны и параллельны их стороны. Следовательно, равны и параллельны диагонали параллелограммов.

В результате сложения двух пар мы получили одну пару сил c тем же плечом и с силами, равными геометрической сумме соответствующих сил слагаемых пар. Найдем момент M этой пары.

Мы пришли к заключению, что для сложения двух пар, лежащих в пересекающихся плоскостях, достаточно сложить их моменты. Но методом доказательства от n к n+1 нетрудно показать, что теорема остается справедливой для любого количества пар сил, т. е.

(25)

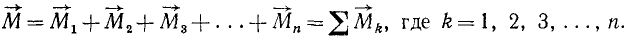
Если сумма моментов всех пар равна нулю, то система пар находится в равновесии, так как наличие такой системы эквивалентно ее отсутствию. Справедливо и обратное заключение: если система пар находится в равновесии, то сумма моментов всех пар системы равна нулю. Таким образом, необходимым и достаточным условием равновесия системы пар, не лежащих в одной плоскости, является равенство нулю геометрической суммы моментов всех пар системы:

(26)

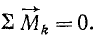
Момент пары является векторной величиной, а потому суммирование надо производить, разумеется, геометрически, т. е. по правилу параллелограмма. В частном, но очень важном случае (имеющем большое применение в технике), когда пары расположены в одной плоскости, сложение моментов производят алгебраически. В самом деле. Будем поворачивать плоскости l и ll на рис. 46 до их совпадения. Тогда угол δ станет равным нулю, параллелограммы выродятся в отрезки прямой и геометрические суммы сил и сумма моментов превратятся в сложение векторов, направленных по прямой, т. е. в алгебраическое сложение.

Поэтому, чтобы сложить пары сил, расположенные в одной плоскости, достаточно алгебраически сложить их моменты:

(25 / )

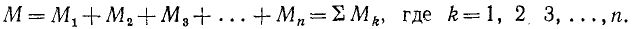
Необходимым и достаточным условием равновесия системы пар, лежащих в одной плоскости, является равенство нулю алгебраической суммы моментов всех пар системы:

(26 / )

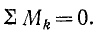
Задача №1

Решение. Требуется определить давление на опоры, но мы будем определять реакции в опорах и рассмотрим для этого равновесие шлюпбалки. Какие же силы действуют на шлюпбалку? На одну шлюпбалку приходится половина веса шлюпки (480 кГ). Эта сила приложена в точке C (рис. 47, б) и направлена вертикально вниз.

В точках А и В на шлюпбалку наложены связи, и в этих точках приложены реакции связей, равные и противоположные давлениям на опоры.

Подшипник В допускает перемещение по вертикали, следовательно, реакция связи, направленная, как известно, перпендикулярно виртуальным перемещениям, горизонтальна. Очевидно, она направлена влево, так как шлюпбалка давит на подшипник вправо.

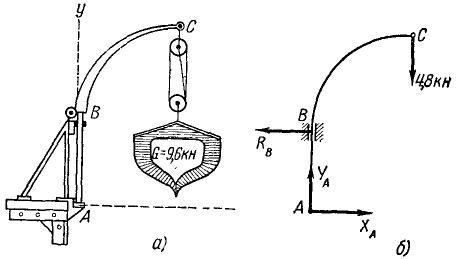
Рис. 47

Направление реакции в шарнире обычно бывает неизвестным, поэтому реакцию в подшипнике разложим на две составляющие Xa и Ya, направленные, как показано на чертеже.

Мы видим, что система сил, приложенных к шлюпбалке, представляет собой две пары сил. Для равновесия такой системы необходимо и достаточно выполнение условия (26)

Заметим, что момент пары (R_B, X_A) положителен, так как эта пара стремится повернуть шлюпбалку против часовой стрелки, а момент (0,5G, Y_A) отрицателен, потому что под действием этой пары шлюпбалка стремится повернуться по ходу часовой стрелки. Из написанного уравнения находим R_B = 640 кГ. Векторы сил пары равны и противоположны, следовательно, реакция X_A = 640 кГ и направлена вправо, реакция Y_A = 480 кГ и направлена вверх, а давления направлены в обратные стороны.

Задача №2

К окружности трех дисков: А — радиуса 15 см (рис. 48, а), В —радиуса 10 см и С—радиуса 5 см приложены пары сил; величины сил, составляющих пары, соответственно равны 10 кГ, 20 кГ и P. Оси OA, OB и ОС лежат водной плоскости. Угол AOB — прямой. Определить величину силы P и угол BOC = а так, чтобы система трех дисков, будучи совершенно свободной, оставалась в равновесии.

Ответ. P = 50 н, α = arctg (—0,75) = 143°10′.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник