что называют абсолютной погрешностью измерения

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

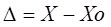
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

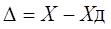
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

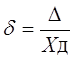
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

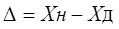
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

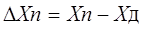
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

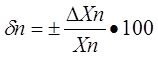
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

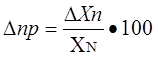
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник

Относительная и абсолютная погрешность – формула определения, как рассчитать погрешность измерения

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 6%. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для отрезка длиной в 10 см погрешность в 1см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1%.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Источник

Глава 1 Измерения и погрешности

1.1 Результат измерения

Рассмотрим простейший пример: измерение длины стержня с помощью линейки. Линейка проградуирована производителем с помощью некоторого эталона длины — таким образом, сравнивая длину стержня с ценой деления линейки, мы выполняем косвенное сравнение с общепринятым стандартным эталоном.

Во-вторых, мы никак не можем быть уверенны, что длина стержня на самом деле такова хотя бы с точностью до ошибки округления. Действительно, мы могли приложить линейку не вполне ровно; сама линейка могла быть изготовлена не вполне точно; стержень может быть не идеально цилиндрическим и т.п.

И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной точности измерения, теряет смысл само понятие «длины стержня». Ведь на масштабах атомов у стержня нет чётких границ, а значит говорить о его геометрических размерах в таком случае крайне затруднительно!

Она показывает, насколько погрешность мала по сравнению с самой измеряемой величиной (её также можно выразить в процентах: ε = δ ⁢ x x ⋅ 100 % ).

О необходимости оценки погрешностей.

Измерим длины двух стержней x 1 и x 2 и сравним результаты. Можно ли сказать, что стержни одинаковы или различны?

В физическом эксперименте (в том числе лабораторном практикуме) оценка погрешностей должна проводиться всегда (даже когда составители задания забыли упомянуть об этом).

1.2 Многократные измерения

Проведём серию из n одинаковых ( однотипных ) измерений одной и той же физической величины (например, многократно приложим линейку к стержню) и получим ряд значений

Что можно сказать о данном наборе чисел и о длине стержня? И можно ли увеличивая число измерений улучшить конечный результат?

По набору результатов 𝐱 можно вычислить их среднее арифметическое:

Это значение, вычисленное по результатам конечного числа n измерений, принято называть выборочным средним. Здесь и далее для обозначения выборочных средних будем использовать угловые скобки.

Кроме среднего представляет интерес и то, насколько сильно варьируются результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как

Разброс данных относительно среднего принято характеризовать среднеквадратичным отклонением :

Будем увеличивать число измерений n ( n → ∞ ). Если объект измерения и методика достаточно стабильны, то отклонения от среднего Δ ⁢ x i будут, во-первых, относительно малы, а во-вторых, положительные и отрицательные отклонения будут встречаться примерно одинаково часто. Тогда при вычислении ( 1.1 ) почти все отклонения Δ ⁢ x i скомпенсируются и можно ожидать, что выборочное среднее при n ≫ 1 будет стремиться к некоторому пределу:

Тогда предельное значение x ¯ можно отождествить с «истинным» средним для исследуемой величины.

Предельную величину среднеквадратичного отклонения при n → ∞ обозначим как

Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр меняется во времени или в результате самого измерения, либо испытывает слишком большие случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не останавливаемся.

Многие случайные величины подчиняются так называемому нормальному закону распределения (подробнее см. Главу 2 ). Для таких величин могут быть строго доказаны следующие свойства:

1.3 Классификация погрешностей

Чтобы лучше разобраться в том, нужно ли многократно повторять измерения, и в каком случае это позволит улучшить результаты опыта, проанализируем источники и виды погрешностей.

В первую очередь, многократные измерения позволяют проверить воспроизводимость результатов: повторные измерения в одинаковых условиях, должны давать близкие результаты. В противном случае исследование будет существенно затруднено, если вообще возможно. Таким образом, многократные измерения необходимы для того, чтобы убедиться как в надёжности методики, так и в существовании измеряемой величины как таковой.

При любых измерениях возможны грубые ошибки — промахи ( англ. miss). Это «ошибки» в стандартном понимании этого слова — возникающие по вине экспериментатора или в силу других непредвиденных обстоятельств (например, из-за сбоя аппаратуры). Промахов, конечно, нужно избегать, а результаты таких измерений должны быть по возможности исключены из рассмотрения.

Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма непрост. В литературе существуют статистические критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем пользоваться (по крайней мере, без серьезного понимания последствий такого отбора). Отбрасывание аномальных данных может, во-первых, привести к тенденциозному искажению результата исследований, а во-вторых, так можно упустить открытие неизвестного эффекта. Поэтому при научных исследованиях необходимо максимально тщательно проанализировать причину каждого промаха, в частности, многократно повторив эксперимент. Лишь только если факт и причина промаха установлены вполне достоверно, соответствующий результат можно отбросить.

Кроме того, удобно разделять погрешности по их происхождению. Можно выделить

Замечание. Разделение погрешностей на систематические и случайные не является однозначным и зависит от постановки опыта. Например, производя измерения не одним, а несколькими однотипными приборами, мы переводим систематическую приборную ошибку, связанную с неточностью шкалы и калибровки, в случайную. Разделение по происхождению также условно, поскольку любой прибор подвержен воздействию «естественных» случайных и систематических ошибок (шумы и наводки, тряска, атмосферные условия и т. п.), а в основе работы прибора всегда лежит некоторое физическое явление, описываемое не вполне совершенной теорией.

1.3.1 Случайные погрешности

Случайный характер присущ большому количеству различных физических явлений, и в той или иной степени проявляется в работе всех без исключения приборов. Случайные погрешности обнаруживаются просто при многократном повторении опыта — в виде хаотичных изменений ( флуктуаций ) значений < x i >.

Если случайные отклонения от среднего в большую или меньшую стороны примерно равновероятны, можно рассчитывать, что при вычислении среднего арифметического ( 1.1 ) эти отклонения скомпенсируются, и погрешность результирующего значения » display=»inline»> ⟨ x ⟩ будем меньше, чем погрешность отдельного измерения.

Случайные погрешности бывают связаны, например,

с особенностями используемых приборов : техническими недостатками (люфт в механических приспособлениях, сухое трение в креплении стрелки прибора), с естественными (тепловой и дробовой шумы в электрических цепях, тепловые флуктуации и колебания измерительных устройств из-за хаотического движения молекул, космическое излучение) или техногенными факторами (тряска, электромагнитные помехи и наводки);

с особенностями и несовершенством методики измерения (ошибка при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером);

с несовершенством объекта измерений (неровная поверхность, неоднородность состава);

со случайным характером исследуемого явления (радиоактивный распад, броуновское движение).

1.3.2 Систематические погрешности

Систематические погрешности, в отличие от случайных, невозможно обнаружить, исключить или уменьшить просто многократным повторением измерений. Они могут быть обусловлены, во-первых, неправильной работой приборов ( инструментальная погрешность ), например, сдвигом нуля отсчёта по шкале, деформацией шкалы, неправильной калибровкой, искажениями из-за не нормативных условий эксплуатации, искажениями из-за износа или деформации деталей прибора, изменением параметров прибора во времени из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации результатов ( методическая погрешность ), например, из-за использования слишком идеализированной физической модели явления, которая не учитывает некоторые значимые факторы (так, при взвешивании тел малой плотности в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических цепях может быть необходим учет неидеальности амперметров и вольтметров и т. д.).

Систематические погрешности условно можно разделить на следующие категории.

Известные погрешности, которые могут быть достаточно точно вычислены или измерены. При необходимости они могут быть учтены непосредственно: внесением поправок в расчётные формулы или в результаты измерений. Если они малы, их можно отбросить, чтобы упростить вычисления.

Погрешности известной природы, конкретная величина которых неизвестна, но максимальное значение вносимой ошибки может быть оценено теоретически или экспериментально. Такие погрешности неизбежно присутствуют в любом опыте, и задача экспериментатора — свести их к минимуму, совершенствуя методики измерения и выбирая более совершенные приборы.

Чтобы оценить величину систематических погрешностей опыта, необходимо учесть паспортную точность приборов (производитель, как правило, гарантирует, что погрешность прибора не превосходит некоторой величины), проанализировать особенности методики измерения, и по возможности, провести контрольные опыты.

Погрешности известной природы, оценка величины которых по каким-либо причинам затруднена (например, сопротивление контактов при подключении электронных приборов). Такие погрешности должны быть обязательно исключены посредством модификации методики измерения или замены приборов.

Наконец, нельзя забывать о возможности существования ошибок, о которых мы не подозреваем, но которые могут существенно искажать результаты измерений. Такие погрешности самые опасные, а исключить их можно только многократной независимой проверкой измерений, разными методами и в разных условиях.

В учебном практикуме учёт систематических погрешностей ограничивается, как правило, паспортными погрешностями приборов и теоретическими поправками к упрощенной модели исследуемого явления.

Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.

Источник

Абсолютная и относительная погрешность

Всего получено оценок: 1757.

Всего получено оценок: 1757.

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Источник