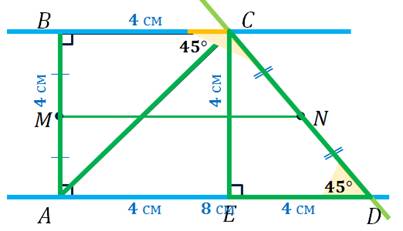
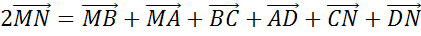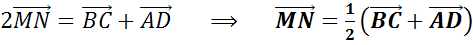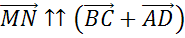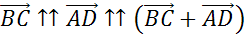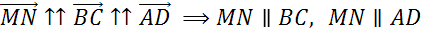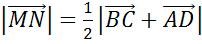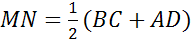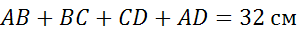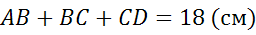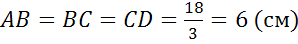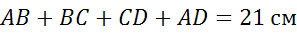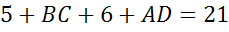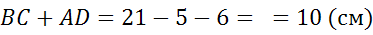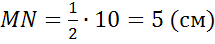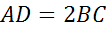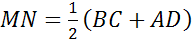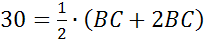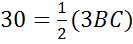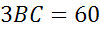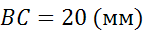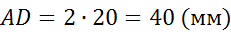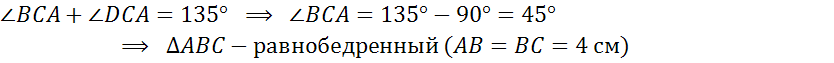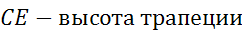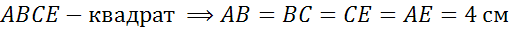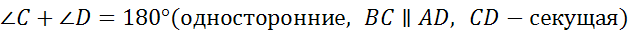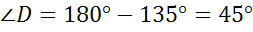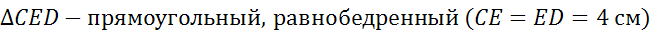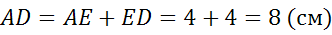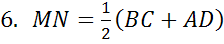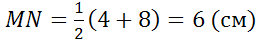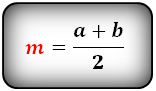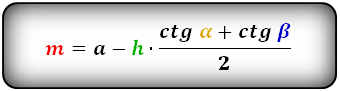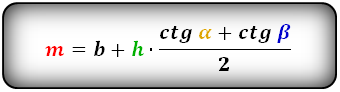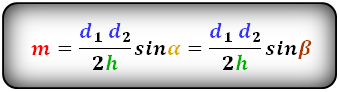что называется средней линией трапеции
Что такое средняя линия трапеции
В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.
Определение средней линии трапеции
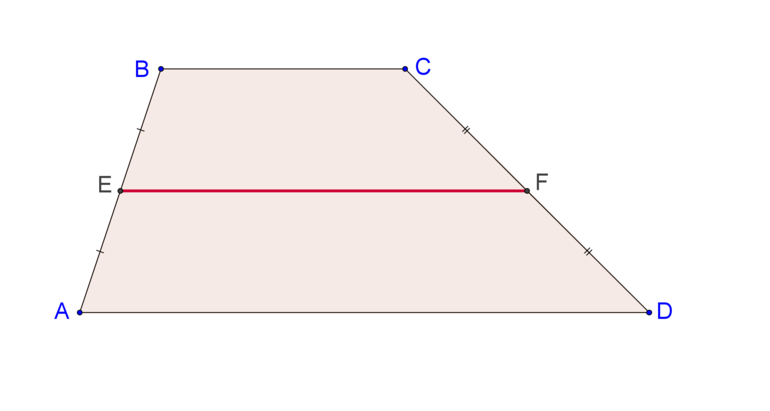
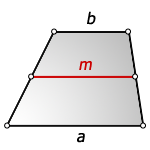
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.
Свойства средней линии трапеции
Свойство 1
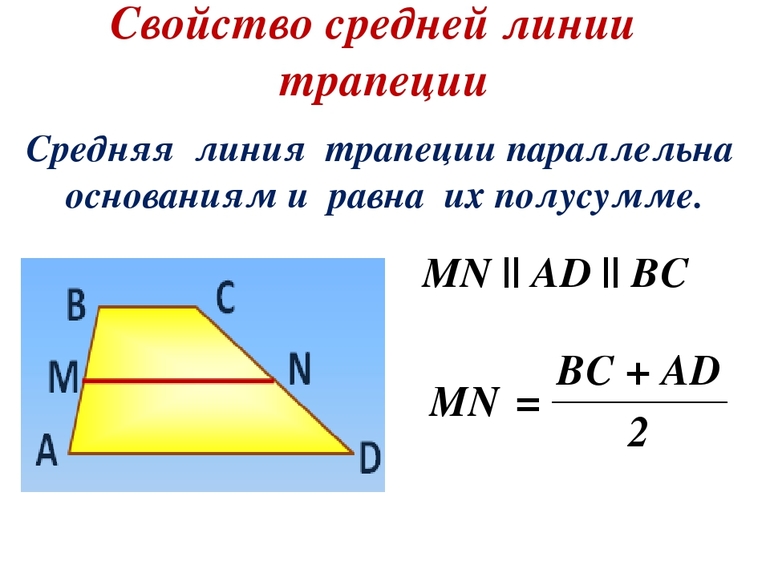
Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.
Свойство 2
Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.
Свойство 3
Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):
Признак средней линии трапеции
Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.
Вторая средняя линия
Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.
Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.
Пример задачи
Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.
Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b) /2 ⋅ h
В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b) /2.
Серединный отрезок
Трапеция — фигура (четырехугольник), что состоит из четырех сторон, две из которых лежат на параллельных прямых, а остальные нет. Параллельные — верхнее и нижнее основание, 2 другие имеют название боковых сторон. Из этого следует, что четырехугольник состоит из двух оснований.
Средняя линия — отрезок, который соединяет середины боков фигуры и обозначается буквой m. Интересно, что если в треугольнике таких отрезков можно провести 3, то в таком четырёхугольнике исключительно одну.
Свойство и формулы
Серединная линия равняется половине сумм длины двух оснований. Это определение является теоремой, доказательство и для того чтобы его сформулировать, необходимо обратить внимание на свойство срединного отрезка в треугольнике.
Доказать теорему просто. Для этого в трапеции проводят серединный отрезок так, чтобы он опускался с верхней точки фигуры и пересекался с продленным нижним основанием. Такая линия делит четырёхугольник на два треугольника. Причем средняя линия фигуры также принадлежит треугольнику и выполняет те же функции. Она равна половине нижней стороны, которая состоит из двух отрезков, равных основаниям трапеции.
Свойство такого отрезка — в четырехугольнике он параллелен основаниям. Учитывая эти данные, их можно использовать как признак при решениях различных заданий для выявления этого понятия.
Формула для нахождения записывается так:
m = (a + b) / 2, где a, b — обозначение длины оснований.
Тригонометрия углов применима в формуле:
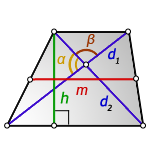
Полусумма оснований трапеции вычисляется через диагонали и их угол пересечения и высоту. Итак, для этого находится:
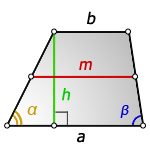
Углы а, b находятся при нижнем основании, а линия h является высотой, проведенной к этому отрезку.
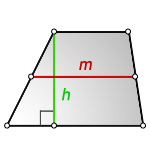
Формула средней линии трапеции через площадь и высоту записывается так:
Кроме этого, такой отрезок делит фигуру на две части и имеет место соотношение их площадей, которое выражается в виде:
Средняя линия трапеции
Урок 10. Геометрия 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Средняя линия трапеции»
Вспомним, какую фигуру называют трапецией.
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называют её основаниями, а две другие — боковыми сторонами.
Известны два частных случая трапеции. Равнобокая трапеция, у которой боковые стороны равны. И прямоугольная трапеция, у которой один из углов прямой.
К слову, у такой трапеции будет два прямых угла.
Повторив определение трапеции, введём понятие средней линии трапеции.
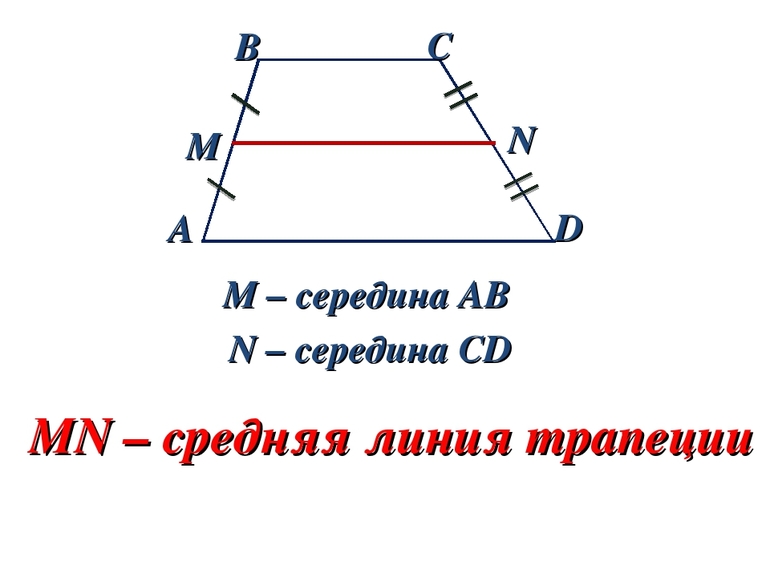
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
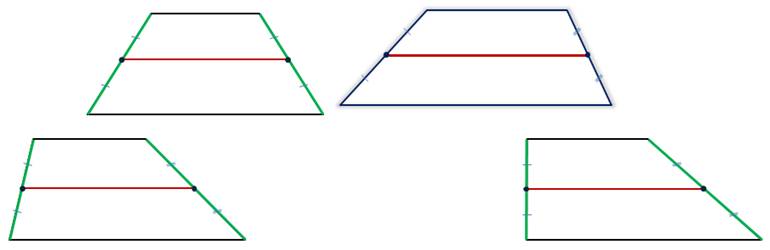
Изобразим средние линии трапеций изображённых на рисунке.
Для этого сначала найдём их боковые стороны. Далее отметим точками их середины. Ну, а потом проведем средние линии.
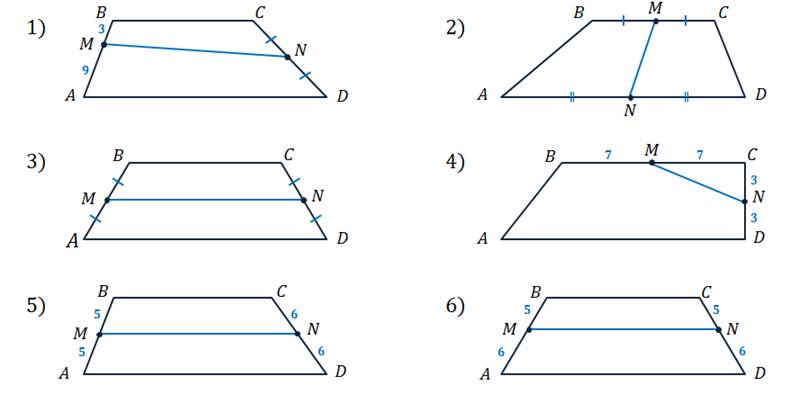
Выполним задание. Пользуясь данными рисунков, указать пункты, в которых 
На первом рисунке точка М не является серединой боковой стороны AB, поэтому МN не является средней линией трапеции.
На втором рисунке точки М и N — середины сторон BC и AD, но они являются основаниями трапеции. А по определению средняя линия трапеции соединяет середины боковых сторон. Значит, в данном случае МN не является средней линией.
На третьем рисунке видим, что точки М и N — середины боковых сторон. Причём по рисунку понятно, что эта трапеция — равнобокая.
Так получаем, что МN в данном случае — средняя линия трапеции ABCD.
Посмотрев на следующий рисунок, не трудно заметить, что МN соединяет середину одного из оснований и середину одной из боковых сторон, а не середины боковых сторон. Поэтому МN не является средней линией.
На рисунке под номером 5 точки М и N середины боковых сторон АB и CD трапеции ABCD. Значит, МN — её средняя линия.
В последнем случае точки М и N не поровну делят боковые стороны трапеции, поэтому МN не является её средней линией.
Мы получили, что только на рисунках под номерами 3 и 5 изображены средние линии трапеции.
Как и средняя линия треугольника, средняя линия трапеции обладает определёнными свойствами.
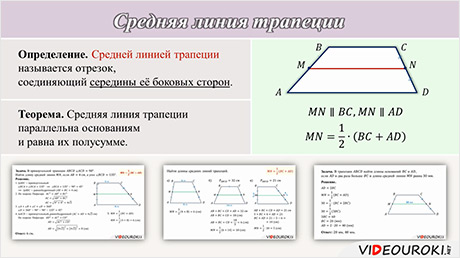
Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
1.
2.
Что и требовалось доказать.
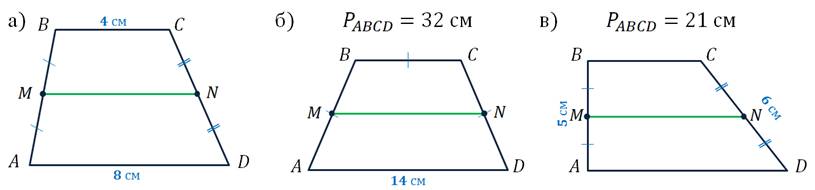
Выполним задание, где, пользуясь этой теоремой и данными рисунков, найдём длины средних линий трапеций.
Длина средней линии трапеции равна полусумме оснований.
На рисунке а известны длины оснований. Поэтому не составит никакого труда найти, что 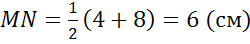
Перейдём к рисунку б.
Известен периметр трапеции, тогда можем записать,
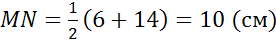
В последнем случае также дан периметр трапеции и известны боковые стороны.
Записав периметр через стороны, и, подставив известные значения, можем выразить сумму оснований.
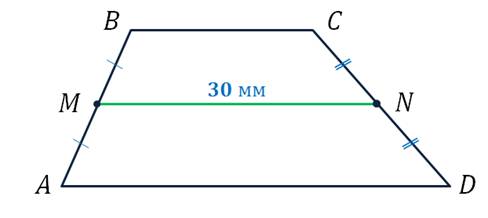
Задача. В трапеции 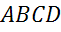
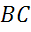
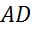
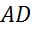
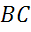
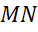
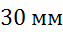
Ответ: 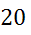
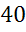
Задача. В прямоугольной трапеции 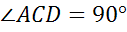
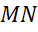
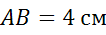
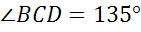
1.
2.
3.
4.
5.
Ответ: 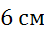
Подведём итоги нашего урока.
Сегодня мы познакомились с понятием средней линии трапеции. Это отрезок, соединяющий середины её боковых сторон.
При этом мы выяснили, что средняя линия трапеции обладает следующими свойствами: она параллельна основаниям трапеции и равна их полусумме.
Так же мы рассмотрели примеры применения этих знаний при решении задач.
Трапеция
Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.
Элементы трапеции
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.
В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.
Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.
Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.
Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
является центром вписанной, и центром описанной окружностей.
Виды трапеции
Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.
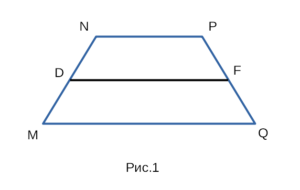
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.
В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.
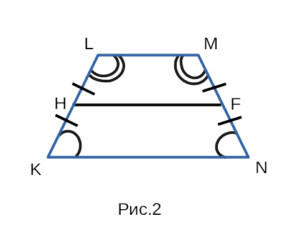
В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.
Все формулы средней линии трапеции
1. Формула средней линии трапеции через основания
Формула средней линии, ( m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
Формулы средней линии трапеции, ( m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
4. Формула средней линии трапеции через площадь и высоту