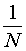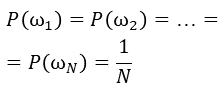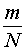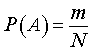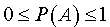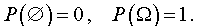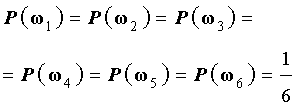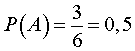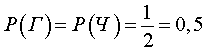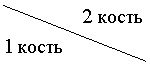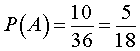что называется пространством элементарных событий

Пространство элементарных событий. Определение вероятности

п.1. Опыт(испытание) и событие (исход)

Выпадение орла или решки

Попадание в 10 или в 9,… на мишени, или в молоко, или выстрел мимо мишени

Подбрасывание игрального кубика

Выпадение 6 или 5,… или 1

Выбор карты из колоды

Выбор пикового туза или любой другой из 54 карт

Ставка при игре в рулетку

Выигрыш на «7 красное» или любой другой из ставок

Событие называется достоверным, если оно обязательно произойдёт в условиях данного опыта.
Событие называется возможным (случайным), если в результате опыта оно может появиться, но может и не появиться.
Событие называется невозможным, если оно не может произойти в условиях данного опыта.
Например:
1) При бросании кубика выпадение 2 – это возможное событие, а выпадение 8 – невозможное. Достоверное событие «1 или 2 или 3 или 4 или 5 или 6».
2) При бросании монеты выпадение орла – это возможное событие, а зависание монеты в воздухе – невозможное. Достоверное событие «орёл или решка».

События называют несовместными, если они не могут произойти одновременно в результате одного опыта.
Например:
1) Нельзя одновременно A=«попасть в 10» и B=«промахнуться» при стрельбе. События A и B – несовместны.
2) Нельзя одновременно C=«достать белый шарик» и D=«достать черный шарик» из коробки. События C и D – несовместны.

События называют равновозможными, если по условиям опыта ни одно из событий не имеет преимуществ перед другими при появлении.

п.2. Пространство элементарных событий

Например:
Пусть при бросании кубика A= <1;3;5>– выпадение нечётного числа. Событие A будет происходить каждый раз при наблюдении элементарных событий 1 или 3 или 5.

п.3. Классическое определение вероятности

Данное определение сформулировано Лапласом в 1795 г. в курсе лекций «Опыт философии теории вероятностей».
Рассмотрим пространство элементарных событий, которое состоит из конечного числа элементарных исходов:

п.4. Геометрическое определение вероятности

Недостатком классического определения вероятности является требование конечности множества событий.
Но нам известны удачные модели бесконечных множеств, которые используются даже в элементарной математике: числовые прямые, системы координат на плоскости и в пространстве. Попробуем их использовать.
Например, рассмотрим опыт со стрельбой в мишень радиуса R=1. Пусть стрелок всегда попадает в мишень. Пространство элементарных событий ограничено кругом x 2 + y 2 ≤1. Круг содержит в себе бесконечное множество точек и все возможные исходы (свойство полноты). Случайное попадание в эту область равновероятно для любой точки (свойство равновозможности). Одновременно попасть в две разные точки области невозможно (свойство несовместности).
Пусть событие A, которое нас интересует, описывается другим ограничением: попаданием в круг \(\mathrm< \left(x-\frac12\right)^2+y^2\leq \frac14. >\)
Тогда:

\begin \mathrm< \Omega: x^2+y^2\leq 1,\ \ \left(x-\frac12\right)^2+y^2\leq \frac14. >\\ \mathrm< S_A=\frac<\pi r^2><2>=\frac<\pi><2>\cdot \frac14=\frac<\pi> <8>>\\ \mathrm< S_<\Omega>=\frac<\pi r^2><2>=\frac<\pi><2>\cdot 1=\frac<\pi> <2>>\\ \mathrm< P(A)=\frac<\pi><8>:\frac<\pi><2>= \frac14 > \end

Геометрическое определение вероятности можно использовать при моделировании бесконечных множеств любой размерности: от одномерных (прямая, на которой определена длина) до многомерных (N-мерные пространства, на которых определены свои меры) (см. также §38 данного справочника).

п.5. Статистическое определение вероятности

Многочисленные опыты с подбрасыванием монеты показывают, что число выпадений «орла» приближается к 1/2, может быть немного больше или меньше, но никогда не равно половине в точности.

К-во бросков монеты

Частота выпадения орла

В принципе, чем больше будет проведено опытов, тем ближе будет экспериментальная величина к теоретической. Поэтому, с точки зрения статистики:

Такое понимание вероятности очень продуктивно, т.к. позволяет вывести важные теоремы, которые широко используются в статистике и других областях прикладной математики.

В современной математике вероятность определяется аксиоматически, в рамках аксиоматики Колмогорова. Если ваша будущая профессия будет связана с математикой, вам обязательно об этом расскажут.

п.6. Примеры

Пример 1. Из хорошо тасованной колоды в 32 карты выбирается наугад одна карта. Какова вероятность того, что это:
1) туз;
2) карта бубновой масти;
3) либо король, либо дама, либо валет;
4)* какова вероятность, что в данной колоде сверху – пиковая дама?

1) Всего карт n = 32, тузов k = 4
Вероятность выбрать туз: \(\mathrm< P=\frac=\frac<4><32>=\frac<1><8>=0,125 >\)
2) Всего карт n = 32, бубновой масти k = 8
Вероятность выбрать карту бубновой масти: \(\mathrm< P=\frac=\frac<8><32>=\frac<1><4>=0,25 >\)
3) Всего карт n = 32, королей, дам и валетов k = 12
Вероятность выбрать короля, даму или валета: \(\mathrm< P=\frac=\frac<12><32>=\frac<3><8>=0,375 >\)

4) Каждое тасование колоды – это перестановка без повторений (см.§34 данного справочника)
Общее количество возможных перестановок: P₃₂=32!
Если зафиксировать первую карту – пиковую даму, то общее количество возможных перестановок оставшихся карт P₃₁=31! – количество вариантов колод с пиковой дамой наверху.
n = 32!, k = 31!
Искомая вероятность:\(\mathrm< P=\frac=\frac<31!><32!>=\frac<1><32>=0,03125 >\)
Ответ: 1) 0,125; 2) 0,25; 3) 0,375; 4) 0,03125.

Пример 2. В слове «КОРОНАВИРУС» наугад выбирается одна буква.
Какова вероятность, что это буква:
1) гласная;
2) согласная;
3) буква «Р»;
4) буква «Ц».

1) Всего букв n = 11, гласных букв k = 5
Вероятность выбрать гласную букву: \(\mathrm< P=\frac=\frac<5> <11>>\)
2) Всего букв n = 11, согласных букв k = 6
Вероятность выбрать согласную букву: \(\mathrm< P=\frac=\frac<6> <11>>\)
3) Всего букв n = 11, букв «Р» k = 2
Вероятность выбрать букву «Р»: \(\mathrm< P=\frac=\frac<2> <11>>\)
4) Всего букв n = 11, букв «Ц» k = 0
Вероятность выбрать букву «Ц»: \(\mathrm< P=\frac=0 >\) – невозможное событие.
Ответ: \(\mathrm< 1)\ \frac<5><11>;\ 2)\ \frac<6><11>;\ 3)\ \frac<2><11>;\ 4)\ 0. >\)

Пример 4. Деревянный куб покрасили и распилили на 1000 кубиков.
Какова вероятность, что случайно выбранный кубик имеет:
1) три окрашенных грани;
2) две окрашенных грани;
3) одну окрашенную грань;
4) ни одной окрашенной грани?

1) Три окрашенных грани будут иметь кубики на вершинах куба.
Вершин у куба 8, значит k = 8. Вероятность \(\mathrm< P=\frac<8><1000>=0,008>\)
2) Две окрашенных грани будут иметь кубики на ребрах куба, кроме вершин.
Всего ребёр у куба 12, на каждом ребре по 8 кубиков без вершин, k = 12 · 8 = 96.
Вероятность \(\mathrm< P=\frac<96><1000>=0,096>\)
3) Одну окрашенную грань будут иметь кубики на гранях куба, кроме ребер и вершин.
Всего граней у куба 6, на каждой грани по 8 · 8 = 64 внутренних кубика, k = 6 · 64 = 384. Вероятность \(\mathrm< P=\frac<384><1000>=0,384>\)
4) Неокрашенными будут k = 8 · 8 · 8 = 512 кубиков.
Вероятность \(\mathrm< P=\frac<512><1000>=0,512>\)
Ответ: 1) 0,008; 2) 0,096; 3) 0,384; 4) 0,512.

Источник

Что называется пространством элементарных событий

уМЕДХЕФ РПНОЙФШ, ЮФП НЩ ЪБОЙНБЕНУС НБФЕНБФЙЛПК Й ЙНЕЕН ДЕМП ОЕ У ТЕБМШОПУФША, Б МЙЫШ У ЕЈ НБФЕНБФЙЮЕУЛПК НПДЕМША. нЩ Й ВХДЕН ЙЪХЮБФШ ФПМШЛП НБФЕНБФЙЮЕУЛЙЕ НПДЕМЙ, Б РТЙМПЦЕОЙЕ ЙИ Л ТЕБМШОПУФЙ ПУФБЧЙН ОБ ДПМА НБФЕНБФЙЮЕУЛПК Й РТБЛФЙЮЕУЛПК УФБФЙУФЙЛЙ.

рТЙНЕТЩ УПВЩФЙК: — ЧЩРБМП ПДОП ЙМЙ ДЧБ ПЮЛБ; — ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.

рТЙНЕТЩ УПВЩФЙК:
— РТЙ РЕТЧПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
— РТЙ ЧФПТПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
— ОБ ЛПУФСИ ЧЩРБМП ПДЙОБЛПЧПЕ ЮЙУМП ПЮЛПЧ;
— ОБ ПВЕЙИ ЛПУФСИ ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.

фБЛ, ЬЛУРЕТЙНЕОФЩ ЙЪ РТЙНЕТПЧ 1, 2 Й 4 (ОП ОЕ 3) РТЙЧПДСФ Л ДЙУЛТЕФОЩН РТПУФТБОУФЧБН ЬМЕНЕОФБТОЩИ ЙУИПДПЧ.

2. еУМЙ Й ОЕУПЧНЕУФОЩ, ФП ;

еУМЙ УПВЩФЙЕ УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ФП ЧЕТПСФОПУФШ ЬФПЗП УПВЩФЙС ТБЧОСЕФУС ПФОПЫЕОЙА :

ОБЪЩЧБЕНПК ЛМБУУЙЮЕУЛЙН ПРТЕДЕМЕОЙЕН ЧЕТПСФОПУФЙ.

нЩ ЧЙДЙН ФЕРЕТШ, ЮФП РПДУЮЈФ ЧЕТПСФОПУФЙ Ч ЛМБУУЙЮЕУЛПК УИЕНЕ УЧПДЙФУС Л РПДУЮЈФХ ПВЭЕЗП ЮЙУМБ «ЫБОУПЧ» Й ЮЙУМБ ЫБОУПЧ, ВМБЗПРТЙСФУФЧХАЭЙИ ЛБЛПНХ-МЙВП УПВЩФЙА. юЙУМП ЫБОУПЧ УЮЙФБАФ У РПНПЭША ЖПТНХМ ЛПНВЙОБФПТЙЛЙ.

еУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБФШ, ФП УМЕДХЕФ ПВЯСЧЙФШ ДЧБ РПУМЕДОЙИ ЙУИПДБ ПДОЙН Й ФЕН ЦЕ ТЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ, Й РПМХЮЙФШ ОЕ ЮЕФЩТЕ, Б ФТЙ ЙУИПДБ:

рЕТЧЩЕ ДЧБ ЙУИПДБ ЙНЕАФ ЧЕТПСФОПУФЙ РП 1/4, Б РПУМЕДОЙК — ЧЕТПСФОПУФШ 1/4+1/4=1/2.

тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ОБВПТ ЙЪ ЫБТПЧ. нПЦОП ОЕ ХЮЙФЩЧБФШ ЙМЙ ХЮЙФЩЧБФШ РПТСДПЛ УМЕДПЧБОЙС ЫБТПЧ, ЧЕТПСФОПУФШ ОЕ ДПМЦОБ ЪБЧЙУЕФШ ПФ УРПУПВБ РПДУЮЈФБ.

чЩВПТ У ХЮЈФПН РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ЬМЕНЕОФПЧ ОБ НЕУФБИ: РП ФЕПТЕНЕ 2,

Источник

Классическое определение вероятности

Содержание

Случайный эксперимент. Множество элементарных исходов. Случайные события

Например, одним из случайных экспериментов, часто используемых в теории вероятностей, является подбрасывание игральной кости. Результатом этого случайного эксперимента будет количество выпавших очков.

Напомним, что игральная кость – это кубик из однородного материала, грани которого пронумерованы числами 1, 2, 3, 4, 5, 6 при помощи нанесенных на грани кубика точек.

Элементарные события часто называют элементарными исходами или, просто, исходами, а множество всех элементарных событий называют пространством элементарных событий, множеством элементарных исходов или пространством элементарных исходов.

Случайные события часто для простоты называют событиями.

Классическое определение вероятности

Если в результате случайного эксперимента может реализоваться один из нескольких равновозможных вариантов, то используют классическое определение вероятности.

Классическое определение вероятности является краеугольным камнем теории вероятностей и вводится в соответствии со следующей схемой.

Определяется множество элементарных событий (результаты случайного эксперимента).

В классическом определении вероятности в качестве множества элементарных событий Ω используют произвольное множество, состоящее из конечного числа элементов. Элементы множества Ω (элементарные события) обозначают

Вероятность каждого элементарного события полагают равной

Определяются случайные события.

Пустым множеством называют множество, в котором нет ни одного элемента. Пустое множество содержится в любом множестве, то есть является подмножеством любого множества.

Определяется вероятность каждого случайного события.

Если A – случайное событие, то вероятность события A полагают равной числу

Вероятность случайного события A принято обозначать P (A).

Таким образом, справедливо равенство

причем, поскольку числитель в правой части формулы (1) не превосходит знаменателя, то вероятность любого случайного события A заключена в пределах

Примеры решения задач

составляют множество элементарных событий Ω :

Поскольку множество Ω состоит из 6 элементов, то вероятность каждого элементарного события равна :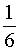

Каждое случайное событие является подмножеством Ω и состоит из нескольких элементарных событий. Так, например, случайное событие

состоит из трех элементарных событий

В силу формулы (4) справедливо равенство

123456123456723456783456789456789105678910116789101112

Источник

Что называется пространством элементарных событий

Определение 5. Событие называется достоверным в опыте G, если при повторении опыта оно происходит всегда. Ему соответствует пространство Ω.

Замечание 4. Случайные события будем обозначать большими латинскими буквами A, B, C и т.д.

Определение 6. Говорят, что в опыте G событие A влечёт появление события B, если из осуществления события A следует наступление события B, т.е. каждый элемент множества A принадлежит множеству B. Это обозначается так: A М B.

2. Алгебра событий

Определение 1. События A и B называются равными A = B, если A М B и B М A.

Определение 2. Суммой событий A и B называется событие A + B состоящее в том, что в опыте произойдёт хотя бы одно из этих событий. Событию A + B соответствует множество, элементы которого принадлежат хотя бы одному из множеств A или B, т.е. объединение множеств A и B.

Определение 3. Произведением событий A и B называется событие AB, состоящее в одновременном появлении этих событий. Событию AB соответствует множество, элементы которого принадлежат одновременно множествам A и B, пересечение множеств A и B.

Определение 4. Разностью событий A и B называется событие A \ B, состоящее в том, что событие A произойдёт, а событие B нет, т.е. событию A \ B соответствует множество, состоящее из элементов множества A, не принадлежащих множеству B.

Определение 5. Событие A называется противоположным событию A, если оно заключается в непоявлении события A. Событию A соответствует множество всех элементов пространства Ω, не принадлежащих множеству A, т.е. A = Ω \ A.

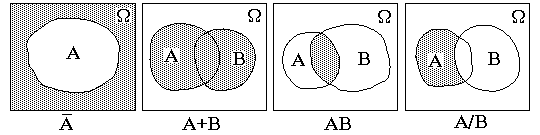
Рисунок 1. Диаграммы Венна

Графические изображения на плоскости соотношений между множествами называются диаграммами Венна.

С в о й с т в а с о б ы т и й A :

3. Вероятность события

Замечание 1. Априори (ранее, до опыта) частота W n (A) является случайной, т.е. нельзя предсказать точное её значение до проведения данной серии из n опытов. Однако природа случайных событий такова, что на практике наблюдается эффект устойчивости частот. Его суть заключается в том, что при увеличении числа опытов значение частоты практически перестаёт быть случайным и стабилизируется около некоторого неслучайного числа P(A), соответствующего данному конкретному событию A в опыте G (точные формулировки приведены в лекции 10, теорема Бернулли Л10.Р2.Т5 ).

С в о й с т в а ч а с т о т ы W n (A) :

Замечание 4. Кроме введённого «частотного» определения вероятности используют также «аксиоматическое». С этой целью введём понятие σ-алгебры.

Аксиомы теории вероятностей :

А3 ( Конечная аддитивность вероятности ). Для любых несовместных событий A и B справедливо равенство P(A+B) = P(A) + P(B).

Источник

Пространство элементарных событий

В этой лекции мы изложим теоретико-множественный подход к основным понятиям теории вероятностей. Пусть проводится некоторый эксперимент со случайным исходом. Результатом эксперимента всегда является один и только один исход из полной группы несовместных событий. Каждый такой исход называют элементарным событием (или элементарным исходом) и обозначают буквой w. Совокупность всех элементарных событий, которые могут появится в эксперименте, называют пространством элементарных событий и обозначают буквой W.

В теоретико-множественной трактовке любое событие А представляет собой некоторое подмножество А=<w> пространства элементарных событий W. Событие А происходит или нет в зависимости от того, принадлежит или нет подмножеству А элементарное событие w, представляющее исход данного опыта. Таким образом, событие А есть подмножество множества W, состоящее из элементарных исходов w, которые благоприятствуют событию А. Поэтому, в дальнейшем, не будем делать различий между событием А и соответствующим подмножеством АÌW.

Среди событий, являющихся подмножеством множества W, можно рассмотреть и само множество W; оно называется достоверным событием. Ко всему пространству W еще добавляется пустое множество Æ; это множество тоже рассматривается как событие и называется невозможным событием.

Для математической формализации модели случайного эксперимента требуется в первую очередь построить пространство элементарных событий W. Однако поскольку понятие «элементарный исход» строго не определено, то задача построения пространства элементарных событий допускает несколько решений. На практике построение такого множества осуществляется из требования, чтобы все интересующие нас результаты данного эксперимента однозначно описывались на основе построенного множества.

Пример 2.1. Пусть эксперимент состоит в подбрасывании один раз игральной кости. Обозначим через X число выпавших очков. Построить пространство элементарных событий W и указать состав подмножеств, соответствующих следующим событиям: A=, B=, C=.

Решение. Очевидно, что за элементарные события здесь лучше всего взять события: <1>, <2>, <3>, <4>, <5>, <6>, которые образуют полную группу несовместных событий. При помощи этих элементарных событий можно легко описать все перечисленные в задаче события:

Отметим, что при решении вероятностных задач построение пространства элементарных событий играет большую роль. Если это пространство построено удачно, то решение задач может значительно упроститься; в противном случае она может представлять значительные трудности или даже вообще не будет найдено. Так, в рассматриваемой задаче за элементарные события можно было бы взять события: w₁=, w₂=, которые также образуют полную группу несовместных событий, т.е. пространство элементарных событий. Однако тогда перечисленные в задаче события невозможно было бы описать.

Алгебра событий

Поскольку при теоретико-множественном подходе к теории вероятностей события отождествляются с множествами, то над событиями можно совершать те же самые операции, что и для множеств. В частности:

Алгебра событий	Алгебра множеств
AÌB	событие А влечет за собой событие В	AÌB	множество А является подмножеством множества В
A=B	событие А тождественно событию В	A=B	равенство множеств
A+B	сумма событий, означающее, что произошло хотя бы одно из двух событий	AÈB	объединение множеств
A×B	произведение событий, означающее, что оба события произойдут одновременно	AÇB	пересечение множеств
A–B	разность событий, означающее, что произойдет событие А, но не произойдет событие В	A \ B	разность множеств, т.е. мно­жество элементов, принадлежащих А, но не принадлежащих В
=W–A	противоположное событие, означающее, что событие А не произойдет	=W \ A	дополнение множества А до W

Действия над событиями становятся более наглядными, если придать им геометрическую интерпретацию в виде диаграмм Вьенна:

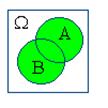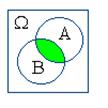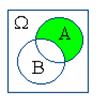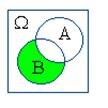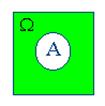A+B	AB	A–B	B–A	

Пример 2.2. Эксперимент состоит в подбрасывании двух игральных костей. Обозначим через X сумму очков, выпадавших на обоих костях. Пространство элементарных событий такого эксперимента можно записать в виде W=<2;3;4;5;6;7;8;9;10;11;12>. Описать следующие события A+B, AB, A–B, B–A, если A==<3;6;9;12>и B==<3;5;7;9;11>. Тогда

Пример 2.3. Пусть имеется колода карт, из которой вынимается одна карта. Описать события AB, B, A+B, A–B, если A=<вынутая карта – туз>, B=<вынутая карта – черви>.

Ответ:

Пример 2.3. Пусть A, B, C – три события, наблюдаемые в некотором эксперименте. Используя алгебру событий, описать следующие события: а) произошло только событие А; б) произошло одно событие; в) произошло хотя бы одно событие.

Ответ:

а) ,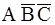

б) ,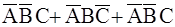

в) A+B+C = .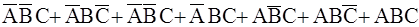

Операции сложения (объединения) и умножения (пересечения) события обладают рядом свойств, аналогичных свойствам обычных операций над числами:

1а. A+B = B+A,	1б. AB = BA,
2а. A+(B+C) = (A+B)+C,	2б. A(BC) = (AB)C.

Это свойства коммутативности и ассоциативности. При этом, пустое множество Æ и само базисное множество W аналогичны нулю и единице, соответственно:

Однако некоторые свойства не имеют аналогов в обычных операциях над числами; в частности:

Это свойства идемпотентности. При введении операций всегда возникает вопрос, какая из двух операций больше «похожа» на сложение, а какая на умножение. Ответ на этот вопрос дают свойства дистрибутивности. Однако для алгебры событий (соответственно, и для алгебры множеств) удивительным образом выполняются оба свойства дистрибутивности:

В теоретико-множественной трактовке эти свойства выглядят более симметрично:

5а. (AÈB)ÇC = (AÇC)È(BÇC),

5б. (AÇB)ÈC = (AÈC)Ç(BÈC).

Эти равенства характеризуют принцип двойственности алгебры событий и показывают равноправие обоих операций. Так, если будет доказана истинность какого-либо тождества, то истинным будет и двойственное ему тождество, т.е. то, которое получается из данного взаимной заменой символов «+» и «×» (или «È» и «Ç»), а также Æ и W. Поэтому все приводимые равенства сгруппированы в пары. Запишем еще несколько свойств:

6а. (AB)+A = A,	6б. (A+B)A = A,
7а. A+ = W,	7б. A = Æ,
8. ` = A,
9а. `Æ = W,	9а. `W = Æ,
10а. A+W = W,	10б. AÆ = Æ,
11а. 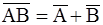,	11б. 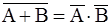.	Законы де Моргана

Система подмножеств множества W, обладающая приведенными свойствами, называется булевой алгеброй. К булевым алгебрам относятся алгебра множеств, алгебра событий и алгебра логики.

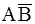
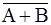
Пример 3.4. Покажите, что события A, и образуют полную группу несовместных событий.

Решение. Покажем, что сумма данных событий образует достоверное событие. Используя законы де Моргана и другие свойства событий, получим:

.

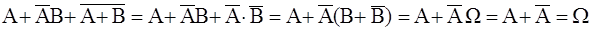
Следовательно, данные события образуют полную группу. Чтобы доказать несовместность данных событий, найдем их попарные произведения:

,

,

.

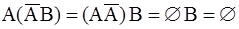
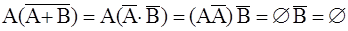
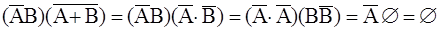
Таким образом, данные в задаче события попарно несовместны. Следовательно, эти события образуют полную группу несовместных события, т.е. образуют пространство элементарных событий.

Источник