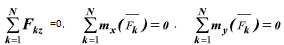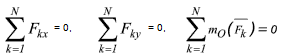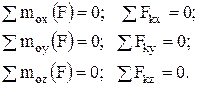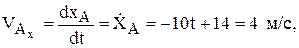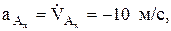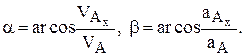что называется произвольной системой сил

iSopromat.ru

Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.

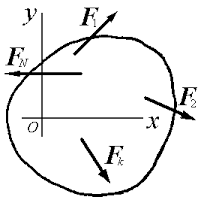
Если все силы, действующие на твердое тело, лежат на одной плоскости, выберем систему координат xOy в плоскости действия сил (рисунок 2.1). В этом случае обнаружим, что

Далее, вспомнив определение момента силы относительно оси, замечаем, что сумма моментов всех сил относительно оси z равна алгебраической сумме моментов этих сил относительно начала координат, т.е. точки О.

В результате останутся следующие три аналитические условия равновесия:

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма моментов всех сил относительно любой точки, лежащих в плоскости действия сил, были равны нулю.

Главным вектором системы сил называется вектор, равный векторной сумме этих сил:

Главным моментом системы сил относительно точки O тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Произвольная система сил

Произвольной будем называть систему сил линии действия, которых расположены как угодно в пространстве. При изучении произвольной системы сил необходимо ознакомиться с понятием момента силы относительно оси.

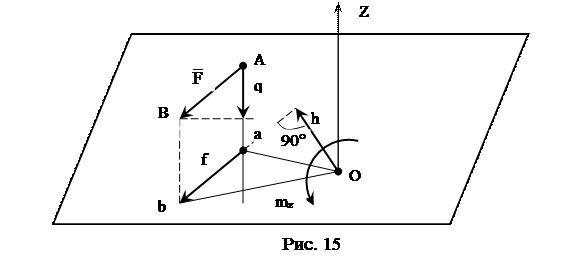
Пусть известна сила F, произвольно расположенная в пространстве. Разложим эту силу на две составляющие: одну параллельную оси Z, и другую f, лежащую на плоскости перпендикулярной оси Z. Опустим перпендикуляр на линию действия силы f и обозначим его h (рис. 15). Мерой вращательного эффекта, создаваемого силой f, будет служить момент силы относительно точки пересечения оси Z с плоскостью. Следовательно, величиной момента силы будет являться взятое с соответствующим знаком произведение m_z = ±f∙h.

Из определения момента и из рис. 15 можно сделать следующие выводы:

1. Момент силы относительно оси равен нулю в том случае, когда линия действия силы пересекает ось или когда сила параллельна этой оси.

2. Момент силы относительно данной оси не изменяется при переносе точки приложения силы в любую другую точку на линии её действия.

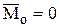
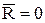
Уравнения равновесия, для произвольно расположенной в пространстве системы сил, получаются из условий, что главный вектор и главный момент равны нулю, т.е. и . Эти уравнения равновесия формулируются следующим образом: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей и суммы моментов относительно этих осей были равны нулю.

Контрольные вопросы:

1. Как Вы сформулируете понятие силы?

2. Что такое реакция связи?

3. Что такое проекция силы на ось?

4. Определить равнодействующую систему сходящихся сил?

5. Условия равновесия системы сходящихся сил.

6. Определить момент силы относительно точки?

7. Что такое пара сил и какими свойствами она обладает?

8. Указать формы условий равновесия плоской системы сил.

9. Каким образом решается задача на систему связанных тел?

10. Как определяется момент силы относительно оси?

11. Условия равновесия произвольной системы сил.

КИНЕМАТИКА

Кинематика является разделом теоретической механики, в котором рассматривается движение тела без учета действующих на него сил. В кинематике решаются следующие задачи: 1) задание движения и изучение кинематических характеристик всего тела; 2) изучение движения каждой из точек в отдельности.

Кинематика точки

Наиболее распространены два способа задания движения точки, причем под точкой часто понимают так называемую материальную точку, т.е. тело, размерами которого в данной задаче можно пренебречь. Последнее справедливо при поступательном (параллельно самому себе) движении тела по прямой и при движении по кривой, когда радиус кривизны траектории много больше размеров тела.

Итак координатный способ предполагает задание координат точки, например точки А, как функций времени.

(1)

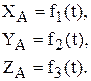
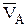
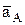
Уравнения движения (1) позволяют построить траекторию, например, по точкам изменяя время с заданным шагом. Они также дают возможность определить скорость и ускорение точки в любой момент времени, как по величине, так и по направлению.

Проекции данных векторов на оси определяются дифференцированием (1) и последующей подстановкой времени, а модули их как корень квадратный из суммы квадратов проекций. При этом, если проекция получается отрицательной, это означает, что соответствующая составляющая вектора направлена против оси (направление осей должно быть задано предварительно, вместе с уравнениями (1)). 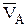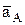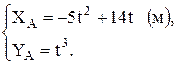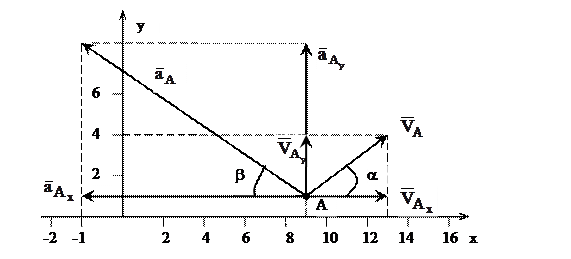Рассмотрим пример определения , при t=1 c, когда (1) имеет вид

,

Тогда из уравнений движения следует (рис. 1)

(2)

(3)

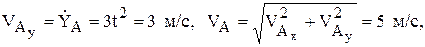
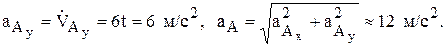
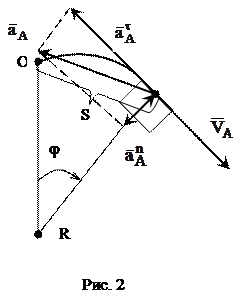
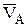
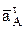
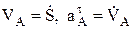
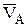
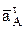
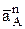
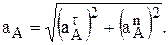
При втором способе задания движения точки, называемом естественным, задают траекторию и начало отсчета пути точки по ней, а так же путь S по траектории в виде функции времени. В этом случае скорость и касательное ускорение всегда касательные к траектории в рассматриваемой точке, а по величине определяются дифференцированием S=f(t), т.е. . Знак «-», полученный после дифференцирования подставки заданного значения времени t, показывает, что данный вектор или направлены в сторону убывания пути или криволинейной координаты S. Полное ускорение точки складывается из касательного и нормального ускорения , которое направлено по нормали (перпендикулярно касательной) в сторону центра кривизны траектории. По величине последнее ускорение зависит от радиуса кривизны траектории в данной точке r, т.е.

(4)

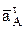
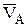
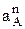
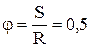
Физический смысл этих двух составляющих полного ускорения в том, что – характеризует интенсивность изменения вектора по величине, а ускорение – по направлению. Рассмотрим пример, когда S=-5t 2 +14t (м) и необходимо определить и при t=1 c, когда траектория точки представляет собой дугу радиусом R=18 м (рис. 2).

S=-5∙1 2 +14∙1 = 9 м, рад » 30°

Если при координатном способе задания движения точки необходимо найти , то используется следующие формулы:

Источник

Тема 1.4. Система произвольно расположенных сил

§1. Приведение пространственной системы сил к данному центру

Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.

Теорема о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы

из точки А (рис. 1, а) в точку О прикладываем в точке О силы и

Рис.1. Произвольной плоской системой сил

Рассмотрим теперь твердое тело, на которое действует какая угодно система сил

Чтобы сложить все полученные пары, надо геометрически сло­жить векторы моментов этих пар. В результате система пар заме­нится одной парой, момент которой или

называется главным моментом системы отно­сительно этого центра.

Рис.2. Система сил

Таким образом мы доказали следующую теорему, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой

Векторы и обычно определяют аналитически, т.е. по их проекциям на оси координат.

Выражения для R_x, R_y, R_z нам известны. Проекции век­тора на оси координат будем обозначать M_x, M_y, M_z. По тео­реме о проекциях суммы векторов на ось будет

Окончательно для определения проекций главного вектора и главного момента получаем формулы:

При этом главный вектор пространственной системы сил: R₀ = ΣP_i отличается от главного вектора плоской системы сил только наличием третьей компоненты, поэтому его модуль будет равен:

В зависимости от значений главного вектора и главного момента, а также от их взаимного расположения возможны следующие варианты приведения пространственной системы сил:

5) R₀ ≠ 0, M₀ ≠0 и главный вектор R₀ неперпендикулярен главному моменту M₀ — система эквивалентна скрещивающимся силам или динаме.

При этом скрещивающимися называются силы, которые непараллельны и не лежат в одной плоскости, а динамой называется система, состоящая из силы и пары сил, плоскость которой перпендикулярна этой силе.

Динама, приложенная к твердому телу, стремится вызвать его винтовое движение, которое представляет совокупность вращательного и поступательного движений.

Примечание: Для пространственной системы сил, как и для плоской, справедлива следующая Теорема Вариньона: Момент равнодействующей пространственной системы сил относительно произвольного центра (оси) равен геометрической (алгебраической) сумме моментов всех сил этой системы относительно данного центра (оси).

§2.Условия равновесия произвольной пространственной системы сил

Источник

Теоретическая механика

9. Плоская система сил. Пара сил. Момент пары сил.

Плоская система сил

Система сил, действующих на плоскости, называется плоской системой сил. Особенностью плоской системы сил заключается в том, что линии действия этих сил уже не пересекаются в одной точке.

Одним из важнейших понятий плоской системы сил является понятие пары сил.

Парой сил называется система двух, равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Согласно аксиоме №1 пара сил не находится в равновесии и не имеет равнодействующую.

Вычисление алгебраического момента пары сил. Для вычисления алгебраического момента пары сил, удобно воспользоваться результатом следующей теоремы.

Теорема. Алгебраическая сумма моментов сил, составляющих пару, относительно любого центра, лежащего в плоскости действия пары сил не зависит от выбора этого центра. Момент пары сил равен произведению одной из сил, составляющих пару на плечо пары.

Пусть в плоскости действует пара сил, как показано на рис.С.24.

Тогда, согласно определению алгебраического момента пары сил и в соответствии с правилом знаков для момента силы относительно центра можно записать

Таким образом, алгебраический момент пары сил не зависит от расстояния до центра и равен произведению модуля силы на плечо пары.

Что и требовалось доказать.

В дальнейшем необходимо рассмотреть следующие теоремы, выражающие основные свойства пар сил и устанавливающие условие эквивалентности двух пар сил.

Теорема. Две пары сил, лежащие в одной плоскости и имеющие численно равные моменты и одинаковое направление вращения, эквивалентны.

Доказательство теоремы проведем в несколько этапов.

4. Согласно теореме Вариньона

Из доказанной теоремы вытекают два важных следствия.

Следствие 1. У данной пары сил, не изменяя оказываемого действия, можно менять величину и направление сил, а также длину плеча, сохраняя при этом величину момента силы.

Следствие 2. Данную пару сил, не изменяя оказываемого действия, можно переносить куда угодно в плоскости действия пары. Следовательно, действие пары на тело не зависит от положения пары в ее плоскости. Таким образом, момент пары является свободным вектором!

Источник

Система произвольно расположенных сил

Содержание:

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Система произвольно расположенных сил в одной плоскости

Теорема о параллельном переносе силы:

Если линии действия сил, приложенные к телу произвольно расположены в одной
плоскости, то такая система сил плоской системой произвольных сил.

Рассмотрим теорему о параллельном переносе силы, которая приложена к телу, которую можно считать леммой. Возьмем произвольное тело, к которому в точке A приложена сила с линией действия MN (рис. 1.17, а). Выберем на теле вторую точку B и проведем через нее прямую, параллельную прямой MN. Приложим на этой прямой в точке B уравновешенную систему сил = –, модули всех трех сил выберем одинаковыми, то есть

Теперь, как видно из рис. 1.17, б, силы и можно объединить в пару сил ( = , //) и ее можно заменить моментом ( ,) пары. Модуль момента этой пары будет равняться моменту данной силы относительно точки В:

Итак, окончательно имеем силу , которая перенесена параллельно в точку В
(сила , = ) и, так называемую, «присоединенную» пару (, ), момент которой
равен моменту силы , переносимой относительно точки B (рис. 1.17, в).

Таким образом, теорему можно сформулировать так: при параллельном переносе силы в другую точку равновесие тела не изменится, если добавить так называемую «присоединенную», или компенсирующую пару, момент которой равен моменту данной силы относительно точки, в которую переносится сила.

Возведение плоской системы произвольных сил к данному центра

Начнем с силы . Сила переносится параллельно самой себе в точку O, но при этом к телу добавляется момент «присоединенной» пары сил, который равен моменту силы относительно точки O:

Теперь мы имели , которая приложена к телу в центре сведения О, присоединенную к телу пару сил с моментом m₁.

Система сходящихся сил в точке O можно заменить одной силой , главным вектором плоской системы произвольных сил. Для этого необходимо геометрически добавить систему сходящихся сил, приложенных в центре сведения O, то есть построить силовой многоугольник (рис. 1.18, б):

Систему пар сил, которая теперь приложена к телу, можно добавить, получив главный момент плоской системы произвольных сил, который равен алгебраической сумме моментов составляющих пар:

Таким образом, плоская система произвольных сил может быть сведена к двум силовым факторам: одной силы — главного вектора системы, и одной пары сил с моментом M — главный момент системы (рис. 1.18, в).

Главный вектор системы равен геометрической сумме векторов составляющих сил, а главный момент системы равен алгебраической сумме моментов всех сил относительно центра сведения.

Главный вектор и главный момент M плоской системы произвольных сил имеют некоторые особенности.

Так, величина главного вектора не зависит от положения центра сведения, а величина главного момента M зависит от изменения центра сводки. А если главный вектор равен нулю, то главный момент M также будет независимым от выбора центра сводки. Если же главный момент M равен нулю, то главный вектор будет равнодействующей плоской системы сил.

Определим аналитически главный вектор и главный момент плоской системы произвольных сил. Для главного вектора сначала определим его проекции на оси плоской декартовой системы координат (в соответствии с теоремой о проекции равнодействующей силы на ось). А именно:

где P_kx, P_ky — проекции k –той силы системы на соответствующие оси координат.

Модуль главного вектора равен

Главный момент M определяется алгебраическим добавлением моментов составляющих сил относительно центра возведения O, а именно:

Некоторые случаи возведения плоской системы произвольных сил к данному центру

Рассмотрим отдельные случаи, которые могут быть при возведении плоской системы произвольных сил к данному центру. А именно:

1. Главный вектор = 0, а главный момент M ≠ 0. В этом случае величина главного момента M не зависит от выбора центра сведения;

2. Главный момент M = 0, а главный вектор ≠ 0. В данном случае главный вектор является равнодействующей силой системы сил;

Теорема Вариньона о моменте равнодействующей системы сходящихся сил

Момент равнодействующей системы сходящихся сил относительно любого центра (точки) равен алгебраической сумме моментов составляющих сил относительно того же центра.

m_o () = 2S∆OAB.

Определим площадь этого треугольника. Как известно, это половина произведения основания (в нашем случае это сторона OA) на высоту треугольника h. А высота в данном случае равна проекции вектора силы на ось х — P_1x. Таким образом, момент силы относительно точки О равен

Аналогично вычислим моменты других сил системы

Теперь перейдем к равнодействующей системы сил и таким же образом определим ее момент относительно точки О. Он будет равняться

m_o () = OA · R_x,

где R_x — проекция равнодействующей силы на ось x.

По теореме о проекции равнодействующей силы на ось, равной алгебраической сумме проекций составляющих сил на эту ось, можно записать

Раскрывая скобки, получим

Таким образом, с последнего выражения видно, что момент равнодействующей силы в отношении любого центра равен алгебраической сумме моментов составляющих сил относительно того же центра.

Условия равновесия тела под действием плоской системы произвольных сил

Как доказано, плоская система произвольных сил всегда может быть сведена к одной силе, которая называется главным вектором системы, и одной пары — главным моментом системы.

Тогда для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный ее момент М равны нулю.

или через проекции главного вектора:

получаем уравнения равновесия:

Таким образом, для равновесия тела, находящегося под действием плоской системы произвольных сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат и сумма моментов всех сил относительно произвольного центра равны нулю.

Существуют две другие формы системы уравнений равновесия плоской системы
произвольных сил. А именно:

Но на эту систему уравнений равновесия накладывается ограничение: прямая, которая может соединить точки A и B, в отношении которых определяются суммы моментов всех сил, не должна быть перпендикулярной оси (в данном случае оси x), на которую проецируются силы.

Третья форма системы уравнений равновесия выглядит

На эту систему уравнений равновесия также накладывается ограничение: точки A, B и C, в отношении которых определяются суммы моментов всеми силами, не должны быть размещены на одной прямой.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник