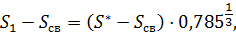что называется приведенным радиусом скважины
МАТЕРИКОВАЯ ДОБЫЧА НЕФТИ
ПОДГОТОВКА СКВАЖИН К ЭКСПЛУАТАЦИИ
Классификация скважин
Процесс течения продукции в пористой среде сопровождается определенными фильтрационными сопротивлениями, которые являются неизвестными. В призабойной зоне скважины возникают дополнительные фильтрационные сопротивления, связанные, вопервых, с наличием самой скважины и, во-вторых, с конкретным ее исполнением.
Для сравнения скважин между собой и оценки каждой конкретной скважины вводятся понятия гидродинамически совершенной скважины и гидродинамически несовершенных скважин.
Под гидродинамически совершенной будем понимать такую скважину, которая вскрыла продуктивный горизонт на всю его толщину h и в которой отсутствуют любые элементы крепи (обсадная колонна, цементный камень, забойные устройства), т.е. скважина с открытым забоем. При течении продукции в такую скважину фильтрационные сопротивления обусловлены только характеристикой продуктивного горизонта и являются минимально возможными.
Большинство реальных скважин относятся к гидродинамически несовершенным. Среди гидродинамически несовершенных скважин выделяют:
Для таких скважин в призабойной зоне возникают дополнительные фильтрационные сопротивления, определяемые видом несовершенства.
Скважины несовершенные по степени вскрытия
Несовершенными по степени вскрытия называются скважины, которые вскрывают продуктивный горизонт не на всю толщину. Дополнительные фильтрационные сопротивления для таких скважин связаны с искривлением линий тока (т.е. геометрии течения) и могут быть учтены введением их в уравнение Дюпюи:
Знаменатель выражения есть фильтрационные сопротивления при течении продукции к совершенной скважине:
Тогда после подстановки получим:
Обозначим дополнительные фильтрационные сопротивления через Rдоп:
Дебит несовершенной по степени вскрытия скважины определится как:
Скважины несовершенные по характеру вскрытия
Несовершенными по характеру вскрытия называются скважины, которые вскрывают пласт на всю толщину, но скважина обсажена и проперфорирована.
Дополнительные фильтрационные сопротивления для таких скважин связаны с изменением геометрии течения продукции вследствие наличия перфорационных отверстий и каналов.
Дебит несовершенной по характеру вскрытия скважины определится из соотношения:
Скважины несовершенные по степени и характеру вскрытия
В этом случае на фильтрационную картину течения продукции к несовершенной по степени вскрытия скважине накладывается фильтрационная картина течения продукции к перфорированным отверстиям и перфорационным каналам.
Для приведенной схемы фильтрационные сопротивления в I области (от Rк до rфс) складываются из:
Для II области (rфс до rс) фильтрационные сопротивления складываются из:
Дебит несовершенной по степени и характеру вскрытия скважины для схематизированной картины течения запишется как:
Для реальной фильтрационной картины:
Коэффициент дополнительных фильтрационных сопротивлений определится как:
Таким образом, коэффициент дополнительных фильтрационных сопротивлений при течении продукции к несовершенной по степени и характеру вскрытия скважине не является простой суммой коэффициентов С1 и С2, а зависит не только от этих коэффициентов, но и относительного вскрытия пласта и радиусов фиктивной (rфс) и реальной (rс) скважин.
Коэффициент гидродинамического совершенства
Любое гидродинамическое несовершенство скважины приводит к снижению дебита. В общем случае дебит несовершенной скважины Qнс запишется в виде:
Коэффициентом гидродинамического совершенства скважины φ называется отношение дебита несовершенной скважины Qнс к дебиту совершенной скважины Qс, и вычисляется по выражению:
Подставив выражение для С получим:
Полученное выражение позволяет оценить вклад каждого вида гидродинамического несовершенства скважин в снижение дебита совершенной скважины. Так, для скважины, несовершенной по степени вскрытия (С2 = 0, rфс = rс), коэффициент гидродинамического совершенства φнсв определится как:
Для скважины, несовершенной по характеру вскрытия (С1 = 0, δ = 1), коэффициент гидродинамического совершенства φнхв определится как:
Приведенный радиус скважины
Дебит фиктивной совершенной скважины определится из соотношения:
Дебит реальной несовершенной скважины, в свою очередь, определится из соотношения:
Приравняв дебет фиктивной совершенной скважины и реальной несовершенной скважины получим:
Таким образом, приведенный радиус скважины связывает между собой радиус реальной скважины с коэффициентом гидродинамического несовершенства С. Численная величина приведенного радиуса скважины может быть определена по результатам исследования скважины на нестационарном режиме.
В настоящее время гидродинамическое совершенство скважин рассчитывается по результатам экспериментального определения приведенного радиуса rпр, что существенно повышает точность, т.к. отпадает необходимость определения коэффициентов C1 и C2 по специальным графикам при заведомо недостоверной информации.
Добыча нефти и газа
Изучаем тонкости нефтегазового дела ВМЕСТЕ!
Приток к несовершенным скважинам
Виды несовершенств скважин. Приведённый радиус. Добавочное фильтрационное сопротивление
Рис. 3.9. Схема притока к несовершенной скважине:
Гидродинамическое несовершенство скважины проявляется в том, что в призабойной зоне пласта с конечной мощностью отсутствует радиальность потока по причине, обусловленной конструкцией забоя или фильтра.
Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта (рис. 3.9,b).
На практике чаще всего встречаются скважины несовершенные как по степени, так и по характеру вскрытия пласта.
Дебит G несовершенной скважины чаще всего меньше дебита Gс совершенной, действующей в тех же условиях, что и данная несовершенная скважина. В некоторых случаях (при торпедной или кумулятивной перфорации, когда глубина прострела достаточно велика) может наблюдаться обратная картина. Отношение данных дебитов d характеризует степень несовершенства скважины и называется параметром несовершенства


Параметр несовершенства зависит от:
* относительного вскрытия пласта 
* плотности перфорации (числа отверстий, приходящихся на 1м фильтра), размеров и формы отверстий;
При расчете несовершенных скважин нередко используют понятие приведенного радиуса несовершенной скважины

где rC – радиус несовершенной скважины, С – коэффициент несовершенства.
Таким образом, вначале находятся приведённые радиусы rпр и дальнейший расчет несовершенных скважин ведется как для совершенных скважин радиуса rпр.

Учитывая (4.40), получаем зависимость между коэффициентом d и и величиной С:

Влияние различного вида несовершенства скважины на приток изучалось как теоретически, так и экспериментально.
3.4.2. Экспериментальные и теоретические исследования притока жидкости к гидродинамически несовершенной скважине
3.4.2.1. Течение по закону Дарси
Для несовершенной по степени вскрытия на основе метода суперпозиции и отображения стоков Маскетом получена зависимость для дебита

Если глубина вскрытия не слишком мала, то формула Маскета даёт хорошие результаты, а так как она проще остальных формул, то ею обычно и пользуются для скважин, несовершенных по степени вскрытия, но совершенных по характеру вскрытия.
Рис. 3.10. График функции
Если толщина пласта много больше радиуса скважины, то для расчета дебитов несовершенной по степени вскрытия скважины можно пользоваться более простой формулой Н.К.Гиринского:

Из зависимости (3.68) видно, что коэффициент несовершенства по степени вскрытия С можно выразить соотношением:

и он добавляется к фильтрационному сопротивлению совершенной скважины.
Если скважины ещё и несовершенны по характеру вскрытия, то коэффициент С увеличивается на величину сопротивления фильтра

3.4.2.2. Течение реального газа по двухчленному закону
В большинстве случаев дебит газовых скважин не следует закону Дарси так же, как в некоторых случаях для нефтяных и водяных скважин.
Вблизи фильтрационных отверстий при приближении к стенке скважины скорость фильтрации становится настолько большой, что число Рейнольдса превосходит критическое. Квадраты скоростей становятся настолько большими, что ими пренебрегать уже нельзя.
Уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине записывается в виде, аналогично идеальному

но здесь А и В являются функциями р и Т

Приток к несовершенной скважине учитывается так же как и при фильтрации по закону Дарси, т.е. введением приведённого радиуса скважины 
Рис.3.11. Схема притока к скважине несовершенной по степени и характеру вскрытия
Для третьей области


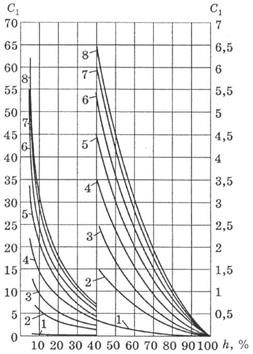
Коэффициент С3 определяется по графикам Щурова, а для определения С4 используется приближенная формула:

где N- суммарное число отверстий; R0- глубина проникновения перфорационной пули в пласт.
Складывая почленно (3.74), (3.75) и уравнение притока для первой области, получим уравнение притока для несовершенной скважины:

Схема размещения добывающих и нагнетательных скважин
Нефтяное месторождение площадью F запланировано разрабатывать с использованием заводнения при площадной семиточечной схеме размещения скважин.
Определение приведенного радиуса скважины. Виды гидродинамического несовершенства скважин и их характерные особенности.
Приведенный радиус скважины – это радиус совершенной (идеальной) скважины, при котором её расчётная продуктивность совпадает с продуктивностью реальной скважины при прочих равных условиях. После подстановки приведённого радиуса вместо реального радиуса в гидродинамические формулы, описывающие фильтрацию к совершенной скважине, эти формулы становятся пригодными для анализа реальной несовершенной скважины.
Существует три типа гидродинамических несовершенства скважины:
1) Если скважина с открытым забоем вскрывает пласт не на всю толщину h, а только на некоторую глубину b, то ее называют гидродинамически несовершенной по степени вскрытия пласта. При этом 
Рис.4. Несовершенная скважина по степени вскрытия пласта
2) Если скважина вскрывает пласт до подошвы, но сообщение с пластом происходит только через специальные отверстия в обсадной колонне и цементном камне или через специальные фильтры, то такую скважину называют гидродинамически несовершенной по характеру вскрытия пласта;
Рис.5. Несовершенная скважина по характеру вскрытия пласта
Рис. 6. Рис. 7.
Графики Щурова
ЗАДАНИЕ
Нефтяное месторождение площадью F запланировано разрабатывать с использованием заводнения при площадной семиточечной схеме размещения скважин.
Результаты геофизических исследований позволяют утверждать, что пласт в пределах нефтенасыщенной площади однороден по проницаемости.
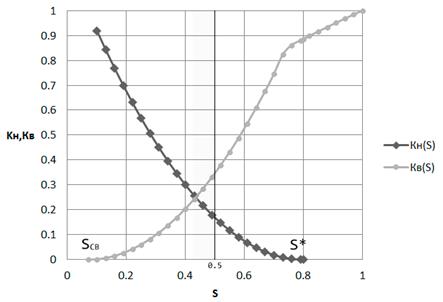
Математическая обработка данных лабораторных экспериментов по вытеснению нефти водой показала, что зависимости относительных фазовых проницаемостей для нефти Кн(S) и воды Кв(S) от водонасыщенности S представляются в виде аналитических соотношений:
При этом Sсв и S* известны. Значение S1 определяется из условия равенства относительных проницаемостей для нефти и воды при S=S1.
В соответствии с проектом разработки в каждую нагнетательную скважину радиусом rнс= 0,1 м закачивается вода с расходом q. Коэффициент охвата пласта заводнением принят по проекту равным Ƞ2.
Добывающие скважины выбывают из эксплуатации при обводненности продукции, равной В.
1) определить изменение во времени добычи нефти, воды, обводненности
продукции и текущей нефтеотдачи для элемента системы разработки и для месторождения в целом;
2) рассчитать динамику среднесуточных дебитов жидкости, нефти и воды
для одной добывающей скважины;
3) определить перепад давления в элементе системы разработки при rв=rнс, rв= rк /2 и rв=rк, если приведенный радиус добывающей скважины rс =0,01м.
РАСЧЕТНАЯ ЧАСТЬ
Исходные данные
площадь месторождения F= 1980⋅10 4 м 2 ;
нефтенасыщенная толщина пласта h0=12 м;
коэффициент пористости m= 0,23;
абсолютная проницаемость К= 0,5 мкм 2 ;
насыщенность связанной водой Sсв= 0,07;
предельная водонасыщенность S * = 0,8;
динамическая вязкость нефти µн= 2 мПа⋅с;
динамическая вязкость воды µв= 1 мПа⋅с;
расход закачиваемой воды q= 500 м 3 /сут;
коэффициент охвата заводнением Ƞ2= 0,74;
время ввода в разработку Т= 2 года;
число элементов площади,
вводимых в эксплуатацию в течение
предельная обводненность В=99 %.
Последовательность расчёта
1. Определение численных значений коэффициента А и параметра S1, входящих в приведенные зависимости Kн(S) и Kв(S).
Значение коэффициента А находим из условия, что Kв(1)=1.

Значение параметра S1 установим из условия:

2. Определим относительные проницаемости нефти и воды в зависимости от водонасыщенности.
Зададимся значениями S от Sсв до 1 и произведём расчеты по формулам (11), (12) и (13), строим график (рис.8), данные расчета заносим в таблицу 1.
| S | Kн | Kв |
| 0,07 | 1,00 | 0,00 |
| 0,10 | 0,92 | 0,00 |
| 0,13 | 0,84 | 0,01 |
| 0,16 | 0,77 | 0,02 |
| 0,19 | 0,70 | 0,03 |
| 0,22 | 0,63 | 0,04 |
| 0,25 | 0,57 | 0,06 |
| 0,28 | 0,51 | 0,08 |
| 0,31 | 0,45 | 0,11 |
| 0,34 | 0,40 | 0,14 |
| 0,37 | 0,35 | 0,17 |
| 0,40 | 0,30 | 0,20 |
| 0,43 | 0,26 | 0,24 |
| 0,46 | 0,22 | 0,29 |
| 0,49 | 0,18 | 0,33 |
| 0,52 | 0,15 | 0,38 |
| 0,55 | 0,12 | 0,43 |
| 0,58 | 0,09 | 0,49 |
| 0,61 | 0,07 | 0,55 |
| 0,64 | 0,05 | 0,61 |
| 0,67 | 0,03 | 0,68 |
| 0,70 | 0,02 | 0,74 |
| 0,73 | 0,01 | 0,82 |
| 0,76 | 0,003 | 0,86 |
| 0,79 | 0,0002 | 0,88 |
| 0,80 | 0,0000 | 0,89 |
| 0,82 | 0,90 | |
| 0,85 | 0,92 | |
| 0,88 | 0,93 | |
| 0,91 | 0,95 | |
| 0,94 | 0,97 | |
| 0,97 | 0,98 | |
| 1,00 | 1,00 |
Данные расчета ОФП
Рис. 8. Зависимость относительных проницаемостей для нефти
Добыча нефти и газа
Изучаем тонкости нефтегазового дела ВМЕСТЕ!
Приток к несовершенным скважинам
Виды несовершенств скважин. Приведённый радиус. Добавочное фильтрационное сопротивление
Рис. 3.9. Схема притока к несовершенной скважине:
Гидродинамическое несовершенство скважины проявляется в том, что в призабойной зоне пласта с конечной мощностью отсутствует радиальность потока по причине, обусловленной конструкцией забоя или фильтра.
Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта (рис. 3.9,b).
На практике чаще всего встречаются скважины несовершенные как по степени, так и по характеру вскрытия пласта.
Дебит G несовершенной скважины чаще всего меньше дебита Gс совершенной, действующей в тех же условиях, что и данная несовершенная скважина. В некоторых случаях (при торпедной или кумулятивной перфорации, когда глубина прострела достаточно велика) может наблюдаться обратная картина. Отношение данных дебитов d характеризует степень несовершенства скважины и называется параметром несовершенства


Параметр несовершенства зависит от:
* относительного вскрытия пласта 
* плотности перфорации (числа отверстий, приходящихся на 1м фильтра), размеров и формы отверстий;
При расчете несовершенных скважин нередко используют понятие приведенного радиуса несовершенной скважины

где rC – радиус несовершенной скважины, С – коэффициент несовершенства.
Таким образом, вначале находятся приведённые радиусы rпр и дальнейший расчет несовершенных скважин ведется как для совершенных скважин радиуса rпр.

Учитывая (4.40), получаем зависимость между коэффициентом d и и величиной С:

Влияние различного вида несовершенства скважины на приток изучалось как теоретически, так и экспериментально.
3.4.2. Экспериментальные и теоретические исследования притока жидкости к гидродинамически несовершенной скважине
3.4.2.1. Течение по закону Дарси
Для несовершенной по степени вскрытия на основе метода суперпозиции и отображения стоков Маскетом получена зависимость для дебита

Если глубина вскрытия не слишком мала, то формула Маскета даёт хорошие результаты, а так как она проще остальных формул, то ею обычно и пользуются для скважин, несовершенных по степени вскрытия, но совершенных по характеру вскрытия.
Рис. 3.10. График функции
Если толщина пласта много больше радиуса скважины, то для расчета дебитов несовершенной по степени вскрытия скважины можно пользоваться более простой формулой Н.К.Гиринского:

Из зависимости (3.68) видно, что коэффициент несовершенства по степени вскрытия С можно выразить соотношением:

и он добавляется к фильтрационному сопротивлению совершенной скважины.
Если скважины ещё и несовершенны по характеру вскрытия, то коэффициент С увеличивается на величину сопротивления фильтра

3.4.2.2. Течение реального газа по двухчленному закону
В большинстве случаев дебит газовых скважин не следует закону Дарси так же, как в некоторых случаях для нефтяных и водяных скважин.
Вблизи фильтрационных отверстий при приближении к стенке скважины скорость фильтрации становится настолько большой, что число Рейнольдса превосходит критическое. Квадраты скоростей становятся настолько большими, что ими пренебрегать уже нельзя.
Уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине записывается в виде, аналогично идеальному

но здесь А и В являются функциями р и Т

Приток к несовершенной скважине учитывается так же как и при фильтрации по закону Дарси, т.е. введением приведённого радиуса скважины 
Рис.3.11. Схема притока к скважине несовершенной по степени и характеру вскрытия
Для третьей области


Коэффициент С3 определяется по графикам Щурова, а для определения С4 используется приближенная формула:

где N- суммарное число отверстий; R0- глубина проникновения перфорационной пули в пласт.
Складывая почленно (3.74), (3.75) и уравнение притока для первой области, получим уравнение притока для несовершенной скважины: