что называется динамической характеристикой асу
Динамические свойства и передаточная функция звеньев АСУ



Для количественной оценки свойств и процессов, происходящих при автоматическом управлении, необходимо знать характеристики и аналитические уравнения, описывающие работу АСУ. Свойства и уравнения системы управления в значительной степени определяются характеристиками и уравнениями входящих в ее состав элементарных звеньев.
Элементарным звеном системы автоматического управления называется искусственно выделяемая ее часть, соответствующая какому-нибудь элементарному алгоритму. В отдельных случаях элементарное звено может объединять несколько устройств, и, наоборот, одно устройство может быть разделено на несколько элементарных звеньев. Элементарное звено характеризует лишь математические зависимости между выходными и входными зависимостями.
Характеристика элементарного звена выражается определенной математической зависимостью между выходной и входной величинами. Определение математических зависимостей между ними и их влияний на процесс регулирования при установившемся состоянии системы составляет статику процесса регулирования. За установившееся состояние принимают такой режим АСУ, в котором разность между фактическим значением управляемой величины и ее заданным значением постоянна во времени.
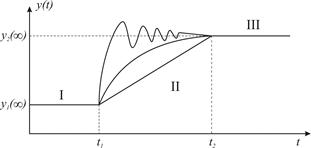
Динамические характеристики определяют свойства звеньев АСУ в переходном процессе, то есть в функции времени, и записываются графически в виде дифференциальных уравнений или передаточных функций, а также в форме частотных характеристик. Под переходным процессом понимается режим перехода системы из одного установившегося состояния к другому при каких-либо воздействиях.
Переходные процессы в линейных звеньях и системах обычно описываются линейными дифференциальными уравнениями. Исследование линейных уравнении значительно проще, чем нелинейных. Переходные процессы в нелинейных звеньях и системах часто трудно поддаются описанию математическими зависимостями или выражаются уравнениями, которые сложно исследовать. Поэтому для анализа нелинейных систем автоматического регулирования применяют различные методы приближенного вычисления или заменяют нелинейные дифференциальные уравнения приближенными линейными. Уравнение системы в целом складывается из уравнений отдельных звеньев. Следовательно, вначале нужно вывести уравнения для звеньев, а затем составить уравнение для всей системы. Форма записи уравнений звеньев и системы в общем одинакова.
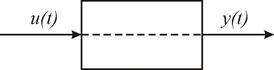
Динамической характеристикой элемента ОУ или всей АСУ называется зависимость выходной (регулируемой) величины y(t) для любого момента времени, от входного воздействия х(t) в переходном режиме. Взаимосвязь выходной и входной величины – называется законом движения, который выражается аналитически в виде дифференциальных уравнений или графически.
Существуют различные способы описания динамических свойств, как отдельных звеньев, так и системы в целом. Чаще других в этих целях применяют дифференциальные уравнения, передаточные функции, временные и частотные характеристики.
При составлении дифференциальных уравнений параметры всех элементов линейных звеньев принимают не зависящими от времени. Чем сложнее звено, тем выше порядок его дифференциального уравнения.
Дифференциальные уравнения при анализировании выражения составляются на основании законов физики, механики, теплотехники, гидравлики, сопромата и других.
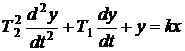
где Т1, Т2 – постоянная времени (постоянные коэффициенты);
х, у – входное и выходное значение регулируемой величины (отклонение входного и выходного воздействия от состояния равновесия)
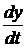
k – коэффициент пропорциональности (коэффициент усиления звена).
В теории автоматического регулирования дифференциальные уравнения для упрощения записи выражаются в операторной форме, при которой операцию дифференцирования по времени 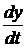
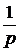
Тогда производную можно представить:
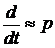
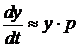
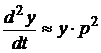
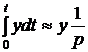
В операторной форме записи дифференциальные уравнения элемента ОУ или всей АСУ в целом, будет иметь вид алгебраического выражения, которое проще анализировать.
В операторной форме выражение (1) примет вид:
В установившемся режиме работы производные выходной величины равны нулю (р = 0), и уравнение упрощается:
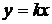
Практически переход от дифференциального уравнения к алгебраическому выполняется без каких-либо вычислений, а формальной заменой 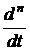

Таким образом, процесс дифференцирования оригинала соответствует умножению на оператор р, а процесс интегрирования – делением на оператор р.
Передаточной функцией называется отношение выходной величины регулируемого параметра к входному значению х в операторной форме записи.
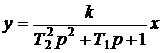
Многочлен, который расположен в знаменателе передаточной функции называется характеристической функцией уравнения элемента или всей АСУ.
Динамические характеристики элементов САУ.
Выше мы получили выражение (2.4), определяющее передаточную функцию линейного элемента системы управления. Это чрезвычайно важное выражение в теории автоматического управления. Оно связывает изображение выходного сигнала Y(s) c изображением входного сигнала Х(s) через динамические свойства элемента системы управления.
Ясно, что входное воздействие может иметь произвольный вид. Однако, чтобы охарактеризовать наиболее существенные черты динамического поведения объекта управления можно использовать некоторые «стандартные» виды входных воздействий. При этом выходной сигнал будет содержать определенную информацию о свойствах объекта управления.
Такие «стандартные» виды воздействий называются типовыми входными воздействиями. К ним относятся:
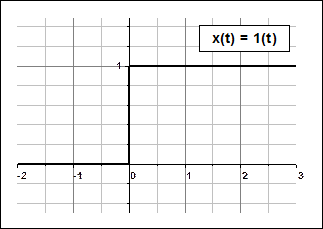
1) Единичная ступенчатая функция: 1(t).
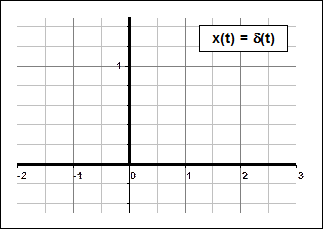
2) Единичная импульсная функция: δ(t).
3) Гармонические функции: sin(ωt) и cos(ωt).
Рис. 2.4. Единичная ступенчатая функция а) и единичная импульсная функция б).
Математически эти функции описываются следующим образом:
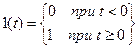
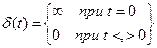
Рис. 2.5. Гармонические функции.
Динамической характеристикой любого элемента системы управления называется его реакция на типовое входное воздействие. В зависимости от вида типового воздействия разделяют временные и частотные характеристики.
§ переходная характеристика h(t);
§ весовая функция или импульсная переходная функция w(t).
7.Динамические характеристики элементов САУ. Частотные характеристики.
§ амплитудно-фазовая частотная характеристика (АФЧХ) или частотная передаточная функция;
§ амплитудная частотная характеристика (АЧХ);
§ фазовая частотная характеристика (ФЧХ);
§ логарифмическая амплитудная частотная характеристика (ЛАЧХ либо ЛАХ);
§ логарифмическая фазовая частотная характеристика (ЛФЧХ либо ЛФХ).
Перечисленные выше характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида. Эти характеристики являются исчерпывающим описанием динамических свойств звена.
Дата добавления: 2016-11-28 ; просмотров: 1280 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ



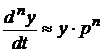
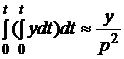

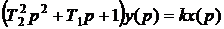
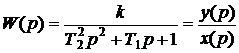
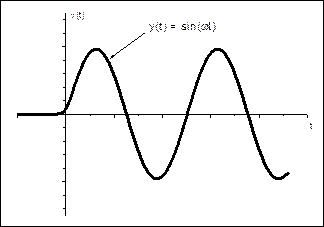
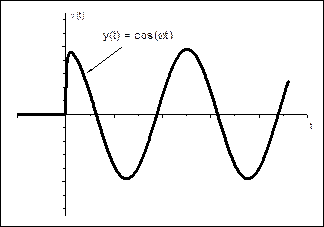
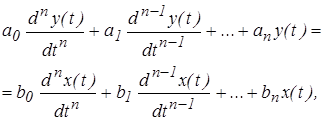 (1)
(1)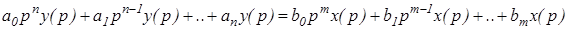
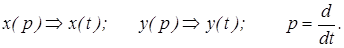
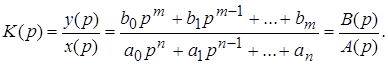 (2)
(2)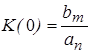 .
.
 .
.
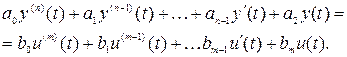 (2.1)
(2.1)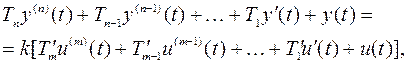 (2.2)
(2.2)